Mathematics

固有値と特異値

つぎの2つの関数は、2,3の特殊な固有値または特異値を計算するのに利用可能です。

関数	詳細
eigs	2,3の固有値
svds	2,3の特異値

これらの関数は、スパース行列と共に頻繁に使われるものです。しかし、これらはフル行列でも可能で、M-ファイルで定義される線形演算子と共にも使うことができます。

ステートメント

[V,lambda] = eigs(A,k,sigma)

は、"シフト"sigmaの近傍に存在する行列A のk個の固有値と対応する固有ベクトルを探します。sigmaを省略すると、大きさの最大の固有値を探します。sigmaがゼロならば、最小の大きさの固有値を探します。2番目の行列Bは、一般化固有問題に対して含まれます。

ステートメント

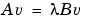
[U,S,V] = svds(A,k)

は、Aのk番目に大きい特異値を求め、

[U,S,V] = svds(A,k,0)

は、k番目に小さい特異値を出力します。

例えば、ステートメント

L = numgrid('L',65);
A = delsq(L);

は、L字型、2次元領域で65行65列のグリッド上に5点Laplace微分演算子を設定します。ステートメント

size(A)
nnz(A)

は、Aは14,473個の非ゼロ要素をもつ2945字の行列を示します。

ステートメント

[v,d] = eigs(A,1,0);

は、最小の固有値と固有ベクトルを計算します。最終的に、

L(L>0) = full(v(L(L>0)));
x = -1:1/32:1;
contour(x,x,L,15)
axis square

は、適切なグリッド点に渡って固有ベクトルの成分を作成し、結果のコンタプロットを作成します。

eigs,svdsで使う数値的な技法は、D.C.Sorensenによる論文[2]に記述されています。この論文は、MATLAB Help Deskでも利用することができます。

連立方程式

参考文献