Mathematics

PDE 問題の表現

この節では、つぎの事柄を説明します。

• MATLAB ソルバpdepeを使って、PDE 問題を解くプロセス
• 指定した点で、解の計算

例題：単純 PDE

つぎの例題は、直接的な定式化、解、単純なPDE の解のプロットに関する事柄を示します。

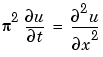
この方程式は、時刻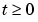に関して、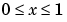 の区間で成り立ちます。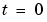で、解は、つぎの初期条件を満足します。

と で、解は、つぎの境界条件を満足します。

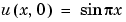
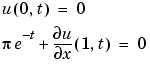
注意    デモ pdex1 は、この例題に対するコードをすべて含んでいます。デモは、単一のM-ファイルの中に、必要なすべてのサブ関数を設定しています。デモを実行するには、コマンドラインで、pdex1 と入力してください。詳細は、PDE ソルバの基本的なシンタックスを参照してください。

1 PDEの書き換え   つぎの型に PDE を書き換えます。

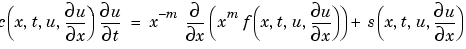
これは、式 17-3で示される型で、pdepeで使用可能なものです。詳細は、 PDE 問題の紹介を参照してください。この例題では、結果の方程式

で、パラメータ と項

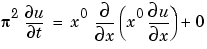
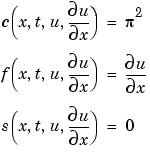
2 MATLAB でのPDE のコード化   上で示される型にPDEを書き直す(式 17-3)し、項を設定すると、pdepeが使用可能な関数に、PDEをコード化できます。関数は、つぎの型をしています。

[c,f,s] = pdefun(x,t,u,dudx)

ここで、c, f, s は、それぞれ、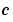, , 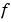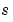の項に対応します。つぎのコードは、例題の問題に対して、c, f, sを計算します。

function [c,f,s] = pdex1pde(x,t,u,DuDx)
c = pi^2;
f = DuDx;
s = 0;

3 初期条件関数をコード化   MATLABの中で、つぎの型の初期条件をコード化します。

u = icfun(x)

つぎのコードは、MATLAB 関数pdex1icに初期条件を表しています。

function u0 = pdex1ic(x)
u0 = sin(pi*x);

4 境界条件関数をコード化   MATLABの中で、つぎの型の境界条件をコード化します。

[pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)

式 17-5と同じ型で記述された境界条件が、つぎのものです。

と

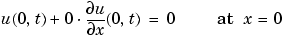
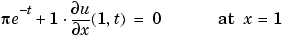
つぎのコードは、MATLAB関数pdex1bcの中の境界条件の要素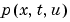 と 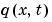を計算するものです。

function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)
pl = ul;
ql = 0;
pr = pi * exp(-t);
qr = 1;

関数 pdex1bc の中で、plと ql は、左の境界条件(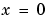) に対応し、prと qr は右の境界条件に対応します()。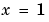

5 解に対するメッシュ点の選択   MATLAB PDE ソルバを使う前に、pdepeを使って、解を計算するメッシュ点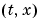を指定する必要があります。これらは、ベクトル t と xで設定できます。

ベクトルt と xは、ソルバの中で、異なる役割を行います(MATLAB の偏微分方程式ソルバを参照)。特に、解のコストと精度は、ベクトルxの長さに強く依存します。しかし、計算は、ベクトルtの中の要素にはあまり影響を受けません。

この例題は、空間区間[0,1] を20等分のメッシュに分割し、時間間隔[0,2]を5等分したtに関して、解を計算します。

x = linspace(0,1,20);
t = linspace(0,2,5);

6 PDE ソルバの適用   例題は、m = 0をもつpdepe、関数 pdex1pde, pdex1ic, pdex1bcをコールし、解を計算する位置を、xとtでメッシュを使って定義します。pdepe関数は、3次元配列solの中に数値解を出力します。ここで、 sol(i,j,k) は、t(i) と x(j)で計算した解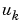の k番目の要素です。

m = 0;
sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);

この例題は、@ を使って、pdex1pde, pdex1ic, pdex1bc に、pdepeへの関数ハンドルとして、渡します。

注意    関数ハンドルに関する情報は、MATLABドキュメントの"MATLAB を使ったプログラミング"のM-ファイルプログラミングや、function_handle (@), func2str, str2func のリファレンスページを参照してください。

7 結果の視覚化   結果を表示することで、例題を終了します。

• 最初の解の成分を抽出し、表示します。この例題で、解 は一成分のみをもっています。しかし、表示目的のために、3次元配列からそれを抽出してみます。サーフェスプロットは、解の挙動を示しています。

u = sol(:,:,1);

surf(x,t,u)    
title('Numerical solution computed with 20 mesh points')
xlabel('Distance x')
ylabel('Time t')

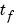• つぎの図は、での解のプロファイルと、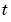の最終値を示しています。この例題で、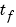 = t = 2になります。詳細は、指定した点での解の計算を参照してください。

figure
plot(x,u(end,:))
title('Solution at t = 2')
xlabel('Distance x')
ylabel('u(x,2)')

指定した点での解の計算

上のように解を得て、プロットした後、tの特別な値での解のプロファイルや、特別な点xでの解の時間変化に興味があります。(ステップ 7の中で抽出した解の)k番目の列u(:,k)は、x(k)での解の時系列を含んでいます。j番目の行 u(j,:) は、t(j)での解のプロファイルを含んでいます。

ベクトルx と u(j,:)と補助関数pdevalを使って、点xoutの任意の組で、解 u と微係数 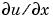を計算します。

[uout,DuoutDx] = pdeval(m,x,u(j,:),xout)

例題 pdex3 は、xout = 0で、解の微係数をpdevalを使って計算します。詳細は、pdevalを参照してください。

MATLAB 偏微分方程式ソルバ

PDE ソルバ性能の改良