Mathematics

PDE問題の紹介

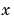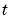つぎの型をした、一つの空間変数と時刻 からなる PDEs をpdepe は解きます。

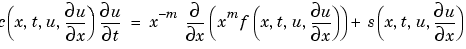
(17-3)

PDE 問題は、 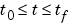と 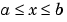で成り立ちます。区間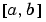は、有限で、 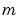は、0, 1, 2 のいずれかで、スラブ、円筒、球面対称も対応します。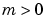の場合、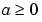もまた成り立ちます。

式 17-3で、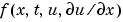は流量の項で、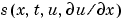はソース項です。時間に関する偏微係数のカップリングは、対角行列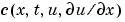との乗算に制限されています。この行列の対角要素は、ゼロ、または、正になります。ゼロの要素は、楕円方程式に対応し、その他は、放物線方程式に対応します。少なくとも、一つは、放物線方程式が存在します。放物線方程式に対応する 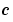の要素は、メッシュ点が存在する場合、 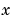の孤立値でゼロになります。メッシュ点が各インタフェースに配置される場合、物質の境界による 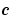と 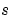の中の不連続部も取り扱えます。

初期時刻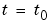で、すべての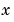に対して、解要素は、つぎの型の初期条件を満足します。

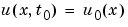
(17-4)

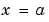、または、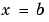の境界で、すべての 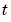に対して、解要素は、つぎの型をした境界条件を満足します。

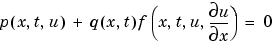
(17-5)

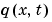は、すべてがゼロか、または、ゼロでないかの要素をもつ対角行列です。境界条件が、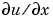より、むしろ、流量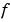の項で表現されることに注意してください。また、2つのパラメータに関しては、 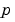のみが、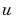に依存します。

PDE 関数のまとめ

MATLAB 偏微分方程式ソルバ