

| Mathematics |   |
MATLAB 偏微分方程式ソルバ
pdepePDE ソルバ
MATLAB PDE ソルバ、pdepeは、一つの空間変数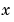 と時間
と時間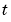 を使って、放物線型、楕円型 PDEsシステムに対する初期値-境界値問題を解きます。システムの中で、少なくとも放物線方程式が一つ必要になります。
を使って、放物線型、楕円型 PDEsシステムに対する初期値-境界値問題を解きます。システムの中で、少なくとも放物線方程式が一つ必要になります。
ユーザが設定するノードをベースに2次の空間的な離散化を使って、pdepe ソルバは、PDEsをODEsに変換します。離散化手法は、[7]に記述されています。時間積分は、ode15sを使って行ないます。 pdepeソルバは、式 17-3 が、楕円方程式を含む場合に生じる微分代数方程式を解くためと指定したスパースパターンをもつヤコビアンの取り扱いに、ode15sの機能を使っています。 ode15s は、時間ステップと定式化をドラマテックに変化させます。
離散化の後、楕円方程式は、代数方程式になります。楕円方程式に対応した初期条件の要素が、離散化と整合性を保っていない場合、pdepe は、時間積分が始まる前にそれらを調整しようとします。このため、最初の時刻に対して出力される解は、他の時間のものと比べて離散化誤差をもっています。メッシュが十分細かい場合、pdepeは、与えられた初期条件に似た整合性のある初期条件を見つけることができます。pdepeが、整合性のある初期条件を見つけることが困難であるメッセージを表示する場合、メッシュをより細かく分割してください。放物線方程式に対応する初期条件ベクトルの要素に対して、調整は必要ありません。
PDE ソルバの基本的なシンタックス
sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan)
| 注意 与えられた対応は、PDE 問題の紹介で使われた項目です。 |
m |
問題の対称性を指定します。 |
pdefun |
PDE の要素を定義します。式 17-3の中の項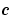 , , 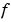 , , 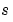 を計算し、つぎの型をしています。 を計算し、つぎの型をしています。x と t はスカラ、u と dudx はベクトルで、解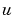 と と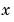 に関するその偏微分係数を近似します。 に関するその偏微分係数を近似します。c, f, s は列ベクトルです。c は、行列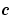 の対角要素を保存します。 の対角要素を保存します。 |
icfun |
初期条件を計算します。つぎの型をしています。xと共にコールすると、icfun は、列ベクトルuの中のxで解要素の初期値を計算し、出力します。 |
bcfun |
境界条件の項 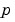 と と 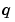 を計算します。つぎの型をしています。 を計算します。つぎの型をしています。ここで、 |
xmesh |
tspan の中のすべての値に対して必要となる数値解に位置を設定するベクトル [x0, x1, ..., xn] 。
x0 と xn は、それぞれ、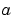 と と 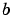 に対応します。 に対応します。解の2次近似は、 xmesh の要素は、x0 < x1 < ... < xnを満足している必要があります。xmesh の長さは、 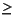 3でなければなりません。 |
tspan |
|
sol(:,:,k) は、解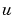 の
のk番目の要素の近似を行ないます。 sol(i,:,k) は、時刻tspan(i) 、メッシュ点xmesh(:)で、解のk番目の要素を近似します。sol(i,j,k) は、時刻tspan(i) とメッシュ点 xmesh(j) で解のk番目の近似を行ないます。PDE ソルバの付加的な引数
よりアドバンスなアプリケーションに対して、入力引数として、ソルバオプションと付加的なパラメータをPDE関数に渡すことができます。
|
オプションパラメータの構造体は、デフォルトの積分プロパティを変更します。これは、7番目の入力引数として設定します。sol = pdepe(m,pdefun,icfun,bcfun,... xmesh,tspan,options)詳細は、PDE ソルバ性能の改良 を参照してください。 |
p1,p2... |
ソルバが、pdefun, icfun, bcfunに渡すパラメータ ソルバは、 options引数の後に設定した任意の入力引数を、pdefun, icfun, bcfun に、コールする度に渡します。オプションがない場合、options = [] を使います。pdefun引数リストの中で、パラメータは、x, t, u, dudxの後に設定されます。 f = pdefun(
icfun 引数リストの中で、パラメータは、xの後に続きます。res = bcfun(x,p1,p2,...) bcfun 引数リストの中で、パラメータは、xl, ul, xr, ur, tの後に続きます。res = bcfun(
例題のデモpdex3を参照してください。 |
 | PDE 問題の紹介 | PDE 問題の表現 |  |