Mathematics

内挿と多次元配列

いくつかの内挿関数は、多次元データにも機能します。

関数	詳細
interp3	3次元データの内挿
interpn	多次元データの内挿
ndgrid	多次元データのグリッド化 (ndfun ディレクトリ)

この節では、つぎの事柄を説明します。

• 3次元データの内挿
• より高次元データの内挿
• 多次元の データのグリッド化

3次元データの内挿

関数interp3は、3次元のサンプル値Vの間の値を探す3次元内挿を行ないます。ユーザは、既知のデータ点をもっていなければなりません。

• X, Y, Z行列は、与えられた値Vの位置を設定します。
• 行列Vは、X, Y, Zの点に対応する値を含んでいます。

interp3に対する最も一般的な型は、

VI = interp3(X,Y,Z,V,XI,YI,ZI,method)

です。ここで、XI, YI, ZIは、関数interp3がVを内挿する点を示すものです。範囲外のものについては、interp3はNaNを出力します。

3次元データの内挿には、3種類のものがあります。

• Nearest neighbor interpolation (method = 'nearest')  この方法は、最も近傍の点を使います。
• Trilinear interpolation (method = 'linear')  この方法は、近傍の8点を使って区分的に線形な内挿を行ないます。
• Tricubic interpolation (method = 'cubic')  この方法は、近傍64点の値を使って区分的にキュービックな内挿を行ないます。

これらすべての方法は、X, Y, Zは共に、特定の方向に増加または減少する単一関数です。加えて、meshgrid関数を使ってこれらの行列を準備するか、またはmeshgridの出力に相当する点のパターンにするかのどちらかを行なってください。

個々の方法は、内挿を行なう前に入力を等間隔の領域に射影します。xが既に等間隔になっているならば、method文字の前に*を付けて実行時間を短縮することができます。例えば、'*cubic'です。

高次元データの内挿

関数interpnは、多次元のサンプルデータVの点間の内挿値を求めるために多次元内挿を行ないます。interpnの最も一般形は、

VI = interpn(X1,X2,X3...,V,Y1,Y2,Y3,...,method)

です。1, 2, 3, ...は、与えられた Vの値に対する点を設定する行列です。 Vは、これらの点に対応する値を含んでいる行列です。1, 2, 3, ...は、interpnがVの内挿された値を出力する点です。範囲外の値に対しては、NaNを出力します。

Y1, Y2, Y3, ... は、同じ大きさの配列かまたはベクトルのどちらかになります。これらが異なる大きさのベクトルならば、interpnは、これらをndgridに転送し、その後、結果の並列を使います。

多次元データに対して3つの異なる方法があります。

• Nearest neighbor interpolation (method = 'nearest')  この方法は、最も近傍な値を使います。
• Linear interpolation (method = 'linear')  この方法は、個々の次元で最も近傍の2つの値を使って区分的に線形な内挿を行ないます。
• Cubic interpolation (method = 'cubic')  この方法は、各々の次元で近傍の4つの値を使って区分的キュービックな内挿を行ないます。

これらすべての方法は、X1, X2,X3 は単調でなければなりません。加えて、ndgrid関数を使ってこれらの行列を準備するか、またはndgridの出力に相当する点のパターンを用意するかのどちらかが必要です。

各々の方法は、内挿が行われる前に入力を等間隔の領域に射影する必要があります。Xが既に等間隔になっているならば、method文字変数の先頭に*を付けることにより実行時間をセーブすることができます。例えば、'*cubic'です。

多次元データのグリッド化

関数ndgridは、多次元関数の関数値や内挿にデータの配列を作成します。ndgridは、一連の入力ベクトルにより設定される領域を一連の出力配列に変換します。これらの出力配列のi番目の次元は、入力ベクトルxiの要素のコピーです。

ndgridの書式は、

[X1,X2,X3,...] = ndgrid(x1,x2,x3,...)

例えば、与えられた範囲に渡り、3つの変数からなる関数を計算しようとします。つぎの関数を考えます。

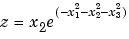
ここで、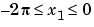, , 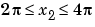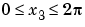の範囲で考えます。この関数を計算し、プロットするには、つぎのようにします。

x1 = -2:0.2:2;
x2 = -2:0.25:2;
x3 = -2:0.16:2;
[X1,X2,X3] = ndgrid(x1,x2,x3);
z = X2.*exp(-X1.^2 -X2.^2 -X3.^2);
slice(X2,X1,X3,z,[-1.2.8 2],2,[-2 0.2]) 

内挿法の比較

散布データの三角メッシュと内挿