| Spline Toolbox | |
Syntax
[pp,p] = csaps(x,y) [pp,p] = csaps(x,y,p) [pp,p] = csaps(x,y,p,[],w) [values,p] = csaps(x,y,p,xx) [values,p] = csaps(x,y,p,xx,w) [...] = csaps({x1,...,xm},y,...)
Description
pp=csaps(x,y)
returns the ppform of a cubic smoothing spline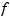 
to the given data x,y, with x and y vectors of the same length. The sequence x of data sites need not be increasing, but if it is not, then it is sorted and the sequence y of data values is correspondingly reordered. After that, x must be strictly increasing.
This smoothing spline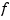 
minimizes
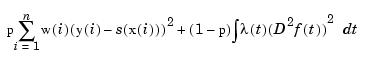
Here,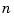 
is the number of entries of x, and the integral is over the smallest interval containing all the entries of x. The default value for the weight vector w in the error measure is ones(size(x)). The default value for the piecewise constant weight function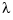 
in the roughness measure is the constant function 1. Further, 
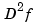denotes the second derivative of the function 
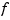. The default value for the smoothing parameter, p, is chosen in dependence on the given data sites x.
pp=csaps(x,y,p)
lets you supply the smoothing parameter. The smoothing parameter determines the relative weight you would like to place on the contradictory demands of having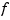 
be smooth vs having 
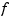be close to the data. For p = 0,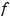 
is the least-squares straight line fit to the data, while, at the other extreme, i.e., for p = 1,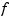 
is the variational, or `natural' cubic spline interpolant. As p moves from 0 to 1, the smoothing spline changes from one extreme to the other. The interesting range for p is often near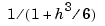 
, with 
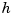the average spacing of the data sites, and it is in this range that the default value for p is chosen. For uniformly spaced data, one would expect a close following of the data for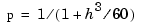 
and some satisfactory smoothing for 
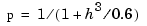. You can input a p > 1, but this leads to a smoothing spline even rougher than the variational cubic spline interpolant.
If the input p is negative or empty, then the default value for p is used. Whether or not you specify the smoothing parameter, you can always obtain the value of p actually used, as the optional second output argument. This is important for experimentation which you might start with [pp,p]=csaps(x,y) in order to obtain a `reasonable' first guess for p.
If you have difficulty choosing p but have some feeling for the size of the noise in y, consider using instead spaps(x,y,tol) which, in effect, chooses p in such a way that the roughness measure
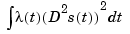
is as small as possible subject to the condition that the error measure
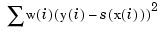
does not exceed the specified tol . This usually means that the error measure equals the specified tol .
The weight function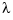 
in the roughness measure can, optionally, be specified as a (non-negative) piecewise constant function, with breaks at the data sites x , by inputing for p a vector whose ith entry provides the value of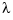 
on the interval (x(i-1) .. x(i)) for i=2:length(x). The first entry of the input vector p continues to be used as the desired value of the smoothness parameter p. In this way, it is possible to insist that the resulting smoothing spline be smoother (by making the weight function larger) or closer to the data (by making the weight functions smaller) in some parts of the interval than in others.
pp = csaps(x,y,p,[],w)
lets you specify the weights w in the error measure, as a vector of nonnegative entries of the same size as x.
[...] = csaps({x1,...,xm},y,...)
provides the ppform of an m-variate tensor-product smoothing spline to data on a rectangular grid. Here, the first argument is a cell-array, containing the vectors x1, ..., xm, of lengths n1, ..., nm, respectively. Correspondingly, y is an array of size [n1,...,nm] (or of size [d,n1,...,nm] in case the data are d-vector-valued), with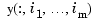
the given (perhaps noisy) value at the grid site 
).
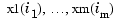In this case, p if input must be a cell-array with m entries or else an m-vector, except that it may also be a scalar or empty, in which case it is taken to be the cell-array whose m entries all equal the p input. The optional second output argument will always be a cell-array with m entries.
Further, w if input must be a cell-array with m entries, with w{i} either empty, to indicate the default choice, or else a nonnegative vector of the same size as xi.
csaps(x,y,p,xx)
is the same as fnval(csaps(x,y,p),xx).
csaps(x,y,p,xx,w)
is the same as fnval(csaps(x,y,p,[],w),xx).
Examples
x = linspace(0,2*pi,21); y = sin(x)+(rand(1,21)-.5)*.1; pp = csaps(x,y, .4, [], [ones(1,10), repmat(5,1,10), 0] );
returns a smooth fit to the (noisy) data that is much closer to the data in the right half, because of the much larger error weight there, except for the last data point, for which the weight is zero.
uses the same data, smoothing parameter, and error weight but chooses the roughness weight to be only .2 in the right half of the interval and gives, correspondingly, a rougher but better fit there, -- except for the last data point which is ignored.
A plot showing both examples for comparison can now be obtained by
fnplt(pp); hold on, fnplt(pp1,'r'), plot(x,y,'ok'), hold off title(['cubic smoothing spline, with right half treated ',... 'differently:']) xlabel(['blue: larger error weights; ', ... 'red: also smaller roughness weights'])
The resulting plot is shown below.
Example 2. As a bivariate example, we add some uniform noise, from the interval [-1/2 .. 1/2], to values of the MATLAB peaks function on a 51-by-61 uniform grid, obtain smoothed values for these data from csaps, along with the smoothing parameters chosen by csaps, and then plot these smoothed values.
x = {linspace(-2,3,51),linspace(-3,3,61)}; [xx,yy] = ndgrid(x{1},x{2}); y = peaks(xx,yy); rand('state',0), noisy = y+(rand(size(y))-.5); [smooth,p] = csaps(x,noisy,[],x); surf(x{1},x{2},smooth.'), axis off
Note the need to transpose the array smooth. For a somewhat smoother approximation, use a slightly smaller value of p than the one, .9998889, used above by csaps. The final plot is obtained by the following:
Algorithm
csaps is an implementation of the Fortran routine SMOOTH from PGS.
The default value for p is determined as follows. The calculation of the smoothing spline requires the solution of a linear system whose coefficient matrix has the form p*A + (1-p)*B, with the matrices A and B depending on the data sites x. The default value of p makes p*trace(A) equal (1-p)*trace(B).
See Also
| | csapi | cscvn | |
