| Spline Toolbox | |
Syntax
Description
pp=csapi(x,y)
returns the ppform of the unique cubic spline s with knot sequence x that takes the value y(:,j) at x(j) for j=1:length(x), and satisfies the not-a-knot end conditions, namely (with
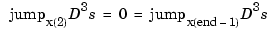
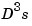the third derivative of 
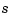). For this, x must be a strictly increasing vector, with as many entries as y has columns. If x is not strictly increasing, it will be sorted, and the columns of y will be re-ordered correspondingly.
If x is a cell array, containing sequences x1, ..., xm, of lengths n1, ..., nm respectively, then y is expected to be an array, of size [n1,...,nm] (or of size [d,n1,...,nm] if the interpolant is to be d-vector-valued). In that case, pp is the ppform of an m-cubic spline interpolant s to such data. In particular, now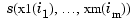 
equals 
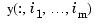for
.
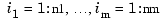You can use the structure pp, in fnval, fnder, fnplt, etc, to evaluate, differentiate, plot, etc, this interpolating cubic spline.
csapi(x,y,xx)
fnval(csapi(x,y),xx), i.e., the values of the interpolating cubic spline at the sites specified by xx are returned.
This command is essentially the MATLAB function spline, which, in turn, is a stripped-down version of the Fortran routine CUBSPL in PGS, except that csapi (and now also spline) accepts vector-valued data and can handle gridded data.
Examples
See the demo csapidem for various examples.
Up to rounding errors, and assuming that x is a vector with at least four entries, the statement pp = csapi(x,y) should put the same spline into pp as the statement
except that the description of the spline obtained this second way will use no break at x(2) and x(n-1).
Here is a simple bivariate example, a bicubic spline interpolant to the Mexican Hat function being plotted:
x =.0001+[-4:.2:4]; y =-3:.2:3; [yy,xx] = meshgrid(y,x); r = pi*sqrt(xx.^2+yy.^2); z = sin(r)./r; bcs = csapi( {x,y}, z ); fnplt( bcs ), axis([-5 5-5 5-.5 1])
Note the reversal of x and y in the call to meshgrid, needed since MATLAB likes to think of the entry z(i,j) as the value at (x(j),y(i)) while this toolbox follows the Approximation Theory standard of thinking of z(i,j) as the value at (x(i),y(j)). Similar caution has to be exerted when values of such a bivariate spline are to be plotted with the aid of the MATLAB mesh function, as is shown here (note the use of the transpose of the matrix of values obtained from fnval).
Algorithm
The relevant tridiagonal linear system is constructed and solved, using the MATLAB sparse matrix capability.
The not-a-knot end condition is used, thus forcing the first and second polynomial piece of the interpolant to coincide, as well as the second-to-last and the last polynomial piece.
See Also
| | csape | csaps | |