Spline Toolbox

csape

Cubic spline interpolation with end conditions

Syntax

• pp = csape(x,y)
  pp = csape(x,y,conds,valconds)
  

Description

pp = csape(x,y) is the ppform of a cubic spline s with knot sequence x that satisfies s(x(j)) = y(:,j) for all j, as well as an additional end condition at the first and at the last data site, namely the default condition listed below.

pp = csape(x,y,conds,valconds) lets you choose the end conditions to be used, from a rather large and varied catalog, by proper choice of conds and valconds. For some choices of conds, valconds need not be present and/or is ignored when present. See below for the possibility of supplying valconds as part of y.

conds may be a string whose first character matches one of the following: 'complete' or 'clamped', 'not-a-knot', 'periodic', 'second', 'variational', with the following meanings.

'complete' or 'clamped'	Match endslopes (as given in valconds, with default as under "default'').
'not-a-knot'	Make second and second-last sites inactive knots (ignoring valconds if given).
'periodic'	Match first and second derivatives at first site with those at last site.
'second'	Match end second derivatives (as given in valconds, with default [0 0], i.e., as in 'variational').
'variational'	Set end second derivatives equal to zero (ignoring valconds if given).
default	Match endslopes to the slope of the cubic that matches the first four data at the respective end (i.e., Lagrange).

By giving conds as a 1-by-2 matrix instead, it is possible to specify different conditions at the two endpoints. Explicitly, the th derivative, , is given the value at the left ( is 1) respectively right ( is 2) endpoint in case is . There are default values for conds and/or valconds.  

Available conditions are:   

clamped	= valconds(j)	if conds(j) == 1
curved	= valconds(j)	if conds(j) == 2
Lagrange		default
periodic		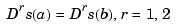if conds == [0  0]
variational		if conds(j) == 2 & valconds(j) == 0

Here, is ( is ), i.e., the first (last) data site, in case j is 1 (j is 2), and (in the Lagrange condition) is the cubic polynomial that interpolates to the given data at 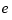and the three sites nearest .

If conds(j) is not specified or is different from 0, 1, or 2, then it is taken to be 1 and the corresponding valconds(j) is taken to be the corresponding default value.

The default value for valconds(j) is the derivative of the cubic interpolant at the nearest four sites in case conds(j) is 1, and is 0 otherwise.

It is possible (and, in the case of gridded data required) to specify valconds as part of y. Specifically, if size(y) is [d,ny] and ny is length(x)+2, then valconds is taken to be y(:,[1 end]), and y(:,i+1) is matched at x(i), i=1:length(x).

It is also possible to handle gridded data, by having x be a cell array containing univariate meshes and, correspondingly, having y be an -dimensional array (or an -dimensional array if the function is to be vector-valued). Correspondingly, conds is a cell array with entries, but the information normally specified by valconds is now expected to be part of y.

This command calls on a much expanded version of the Fortran routine CUBSPL in PGS.

Examples

csape(x,y) provides the cubic spline interpolant with the Lagrange end conditions, while csape(x,y,[2 2]) provides the variational, or natural cubic spline interpolant, as does csape(x,y,'v'). csape([-1 1],[-1 1],[1 2],[3 6]) provides the cubic polynomial for which , , , , i.e., . Finally, csape([-1 1],[-1 1]) provides the straight line p for which p(±1) = ±1, i.e., .

As a multivariate vector-valued example, here is a sphere, done as a parametric bicubic spline, 3D-valued, using prescribed slopes in one direction and periodic side conditions in the other:

• x = 0:4; y=-2:2; s2 = 1/sqrt(2);
  clear v
  v(3,:,:) = [0 1 s2 0 -s2 -1 0].'*[1 1 1 1 1];
  v(2,:,:) = [1 0 s2 1 s2 0 -1].'*[0 1 0 -1 0];
  v(1,:,:) = [1 0 s2 1 s2 0 -1].'*[1 0 -1 0 1];
  sph = csape({x,y},v,{'clamped','periodic'});
  values = fnval(sph,{0:.1:4,-2:.1:2});
  surf(squeeze(values(1,:,:)),squeeze(values(2,:,:)),... 
  squeeze(values(3,:,:))); axis equal, axis off
  

The lines involving fnval and surf could have been replaced by the simple command: fnplt(sph). Note that v is a 3-dimensional array, with v(:,i,j) the 3-vector to be matched at (x(i),y(j)), i=1:5, j=1:5. Note further that, in accordance with conds{1} being 'clamped', size(v,2) is 7 (and not 5), with the first and last entry of v(r,:,j) specifying the end slopes to be matched.

End conditions other than the ones listed earlier can be handled along the following lines. Suppose that we want to enforce the condition

for given scalars , , and , and with equal to x(1). Then one could compute the cubic spline interpolant to the given data using the default end condition as well as the cubic spline interpolant to zero data and some (nontrivial) end condition at , and then obtain the desired interpolant in the form

Here are the (not inconsiderable) details (in which the first polynomial piece of and is pulled out to avoid differentiating all of and ):

• pp1 = csape(x,y);
  dp1 = fnder(fnbrk(pp1,1)); 
  pp0 = csape(x,zeros(size(y)),[1,0],[1,0]); 
  dp0 = fnder(fnbrk(pp0,1));
  e = x(1); 
  lam1 = a*fnval(dp1,e) + b*fnval(fnder(dp1),e); 
  lam0 = a*fnval(dp0,e) + b*fnval(fnder(dp0),e);
  pp = fncmb(pp0,(c-lam1)/lam0,pp1);
  

Algorithm

The relevant tridiagonal linear system is constructed and solved using the sparse matrix capabilities of MATLAB.

See Also

csapi, spapi, spline

Cautionary Note

If the sequence x is not nondecreasing, both x and y will be reordered in concert to make it so. Also, if the value sequence y is vector-valued, then valconds(:,j), j=1:2, must be vectors of that same length (if explicitly given).

chbpnt

csapi