Spline Toolbox

cscvn

"Natural" or periodic interpolating cubic spline curve

Syntax

• curve = cscvn(points)
  

Description

cscvn(points) returns a parametric variational, or natural, cubic spline curve (in ppform) passing through the given sequence

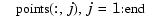. The parameter value 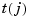for the 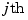point is chosen by Eugene Lee's [1] centripetal scheme, i.e., as accumulated square root of chord length:

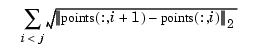
If the first and last point coincide (and there are no other repeated points), then a periodic cubic spline curve is constructed. However, double points result in corners.

Examples

The following provides the plot of a questionable curve through some points (marked as circles):

• points=[0 1 1 0 -1 -1 0 0; 0 0 1 2 1 0 -1 -2]; 
  fnplt(cscvn(points)); hold on, 
  plot(points(1,:),points(2,:),'o'), hold off
  

Here is a closed curve, good for 14 February, with one double point:

• c=fnplt(cscvn([0 .82 .92 0 0 -.92 -.82 0; .66 .9 0 ...
  -.83 -.83 0 .9 .66])); fill(c(1,:),c(2,:),'r'), axis equal
  

Algorithm

The break sequence t is determined as

• t = cumsum([0;((diff(points.').^2)*ones(d,1)).^(1/4)]).';
  

and csape (with either periodic or variational side conditions) is used to construct the smooth pieces between double points (if any).

See Also

csape, fnplt, getcurve, getcurv2, spcrvdem

References

[1]  E.T.Y. Lee, Choosing nodes in parametric curve interpolation, Computer-Aided Design 21 (1989), 363-370.

csaps

fn2fm