| Spline Toolbox | |
Syntax
sp = spaps(x,y,tol) [sp,values] = spaps(x,y,tol)[sp,values,rho] =spaps(x,y,tol)[...] = spaps(x,y,tol,arg1,arg2,...)[...] =spaps({x1,...,xr},y,tol,...)
Description
spaps(x,y,tol)
returns the B-form of the smoothest function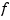 
that lies within the given tolerance tol of the given data x, y. Here, x and y are vectors of the same length. The sequence, x, of data sites need not be increasing, but if it is not, then it is sorted and the sequence, y, of data values is correspondingly reordered.
[sp,values] = spaps(x,y,tol)
also returns the smoothed values, i.e., values is the same as fnval(sp,x).
Here, the distance of the function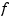 
from the given data is measured by
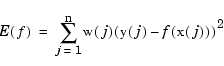
with the default choice for the weights w making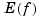 
the composite trapezoidal rule approximation to
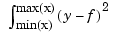
Further, smoothest means that the following roughness measure is minimized:
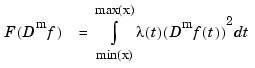
where 
denotes the mth derivative of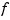 
. The default value for m is 2, and this makes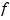 
a cubic smoothing spline.
The data being fitted may be d-vector-valued, and this is indicated by having y be of size [d,n]. In this case,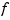 
is also d-vector-valued. We replace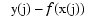 
in the error measure by the Euclidean norm 
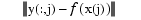of the error at the site x(j). Likewise, we replace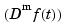 
in the roughness measure by its Euclidean norm 
.
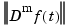When tol is nonnegative, then the spline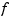 
is determined as the unique minimizer of the expression 
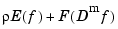, with the smoothing parameter 
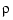(optionally returned) so chosen that 
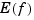equals tol. Hence, when m is 2, then, after conversion to ppform, the result should be the same (up to roundoff) as obtained by
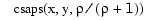. Further, when tol is zero, then the ``natural'' or variational spline interpolant of order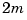 
is returned. For large enough tol, the least-squares approximation to the data by polynomials of degree <m is returned.
When tol is negative, then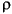 
is taken to be -tol.
The default value for the weight function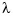 
in the roughness measure is the constant function 1. But you may choose it to be, more generally, a piecewise constant function, with breaks only at the data sites. Assuming the vector x to be strictly increasing, you specify such a piecewise constant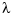 
by inputting tol as a vector of the same size as x. In that case, tol(i) is taken as the constant value of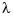 
on the interval (x(i-1) .. x(i)), i=2:length(x), while tol(1) continues to be used as the specified tolerance.
[sp,values,rho] = spaps(x,y,tol)
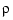used as the third output argument.
[...] = spaps(x,y,tol,arg1,arg2,...)
lets you specify the weight vector w and/or the integer m, by supplying them as an argi. For this, w must be a nonnegative vector of the same size as x. m must be 1 (for a piecewise linear smoothing spline), or 2 (for the default cubic smoothing spline), or 3 (for a quintic smoothing spline).
[...] = spaps({x1,...,xr},y,tol,...)
returns the B-form of an r-variate tensor-product smoothing spline that is within the specified tolerance to the given gridded data. Now y is expected to supply the corresponding gridded values, with size(y) equal to [length(x1),...,length(xr)] in case the function is scalar-valued, and equal to [d,length(x1),...,length(xr)] in case the function is d-vector-valued. Further, tol must be a cell array with r entries. The optional input for m must be an r-vector (with entries from the set {1,2,3}), and the optional input for w must be a cell array of length r, with w{i} either empty (to indicate that the default choice is wanted) or else a positive vector of the same length as xi.
Examples
give a quintic smoothing spline approximation to the given data that close to interpolates the first and last datum, while being within about 1.e-2 of the rest.
x = -2:.2:2; y=-1:.25:1; [xx,yy] = ndgrid(x,y); rand('seed',39); z = exp(-(xx.^2+yy.^2)) + (rand(size(xx))-.5)/30; sp = spaps({x,y},z,8/(60^2)); fnplt(sp), axis off
produces the figure below, showing a smooth approximant to noisy data from a smooth bivariate function. Note the use of ndgrid here; use of meshgrid would have led to an error.
Algorithm
Reinsch's approach [1] is used (including his clever way of choosing the equation for the optimal smoothing parameter in such a way that a good initial guess is available and Newton's method is guaranteed to converge and to converge fast).
See Also
References
[1] C. Reinsch, ``Smoothing by spline functions'', Numer. Math. 10 (1967), 177- 183.
| | spapi | spcol | |
