| Spline Toolbox | |
Syntax
Description
tpaps(x,y)
is the stform of a thin-plate smoothing spline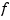 
for the given data sites x(:,j) and the given data values y(:,j). The x(:,j) must be distinct points in the plane, and x and y must have the same number of columns.
The thin-plate smoothing spline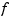 
is the unique minimizer of the weighted sum
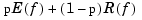
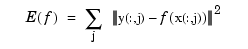
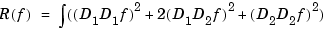
Here, the integral is taken over all of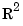 
, and 
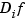denotes the partial derivative of 
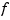with respect to its 
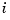th argument, hence the integrand involves second partial derivatives of 
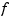. The smoothing parameter p is chosen in an ad hoc fashion.
tpaps(x,y,p) also inputs the smoothing parameter, p, a number between 0 and 1. As the smoothing parameter varies from 0 to 1, the smoothing spline varies, from the least-squares approximation to the data by a linear polynomial when p is 0, to the thin-plate spline interpolant to the data when p is 1.
[f,p] = tpaps(...) also returns the smoothing parameter actually used.
Examples
Example 1. The following code obtains values of a smooth function at 31 randomly chosen sites, adds some random noise to these values, and then uses tpaps to recover the underlying exact smooth values. To illustrate how well tpaps does in this case, the code plots, in addition to the smoothing spline, the exact values (as black balls) as well as each arrow leading from a smoothed value to the corresponding noisy value.
rand('seed',23); nxy = 31; xy = 2*(rand(2,nxy)-.5); vals = sum(xy.^2); noisyvals = vals + (rand(size(vals))-.5)/5; st = tpaps(xy,noisyvals); fnplt(st), hold on avals = fnval(st,xy); plot3(xy(1,:),xy(2,:),vals,'wo','markerfacecolor','k') quiver3(xy(1,:),xy(2,:),avals,zeros(1,nxy),zeros(1,nxy), ... noisyvals-avals,'r'), hold off
Example 2. The following code uses an interpolating thin-plate spline to vector-valued data values to construct a map, from the plane to the plane, that carries the unit square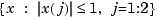 
pretty much onto the unit disk 
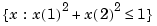, as shown by the picture generated.
n = 64; t = linspace(0,2*pi,n+1); t(end) = []; values = [cos(t); sin(t)]; centers = values./repmat(max(abs(values)),2,1); st = tpaps(centers, values, 1); fnplt(st), axis equal
Note the choice of 1 for the smoothing parameter here, to obtain interpolation.
Limitations
The determination of the smoothing spline involves the solution of a linear system with as many unknowns as there are data points. Since the matrix of this linear system is full, the solving can take a long time even if, as is the case here, an iterative scheme is used when there are more than 728 data points. The convergence speed of that iteration is strongly influenced by p, and is slower the larger p is. So, for large problems, use interpolation, i.e., p equal to 1, only if you can afford the time.
See Also
| | stmak | Glossary | |
the error measure
the roughness measure
