Spline Toolbox

fnplt

Plot a function

Syntax

• fnplt(f)
  fnplt(f,arg1,arg2,arg3,arg4) 
  

points = fnplt(f)

Description

fnplt(f) plots the function, described by f, on its basic interval.

If 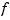is univariate, the following is plotted:

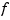• If is scalar-valued, the graph of 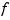is plotted.
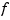• If is 2-vector-valued, the planar curve is plotted.
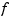• If is 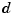-vector-valued with 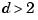, the space curve given by the first three components of 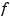is plotted.

If 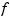is bivariate, the following is plotted:

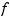• If is scalar-valued, the graph of 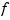is plotted (via surf).
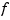• If is 2-vector-valued, the image in the plane of a regular grid in its domain is plotted.
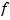• If is 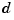-vector-valued with 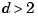, then the parametric surface given by the first three components of its values is plotted (via surf).

If 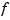is a function of more than two variables, then the bivariate function, obtained by choosing the midpoint of the basic interval in each of the variables other than the first two, is plotted.

fnplt(f,arg1,arg2,arg3,arg4) permits you to modify the plotting by the specification of additional input arguments. You can place these arguments in whatever order you like, chosen from the following list:

• A string that specifies a plotting symbol, such as '-.' or '*'; the default is '-'.
• A scalar to specify the linewidth; the default value is 1.
• A string that starts with the letter 'j' to indicate that any jump in the univariate function being plotted should actually appear as a jump. The default is to fill in any jump by a (near-)vertical line.
• A vector of the form [a,b], to indicate the interval over which to plot the univariate function in f. If the function in f is 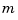-variate, then this optional argument must be a cell array whose ith entry specifies the interval over which the ith argument is to vary. In effect, for this arg, the command fnplt(f,arg,...) has the same effect as the command fnplt(fnbrk(f,arg),...). The default is the basic interval of f.
• An empty matrix or string, to indicate use of default(s). You will find this option handy when your particular choice depends on some other variables.

points = fnplt(f,...) plots nothing, but the two-dimensional points or three-dimensional points it would have plotted are returned instead.

Algorithm

The univariate function 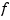described by f is evaluated at 101 equally spaced sites x filling out the plotting interval. If 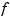is real-valued, the points 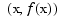are plotted. If 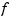is vector-valued, then the first two or three components of 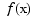are plotted.

The bivariate function 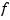described by f is evaluated on a 51-by-51 uniform grid if 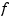is scalar-valued or 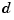-vector-valued with 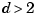and the result plotted by surf. In the contrary case, 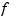is evaluated along the meshlines of a 11-by-11 grid, and the resulting planar curves are plotted.

See Also

fnder, fnint, fnval

Cautionary Note

The basic interval for 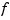in B-form is the interval containing all the knots. This means that, e.g., 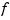is sure to vanish at the endpoints of the basic interval unless the first and the last knot are both of full multiplicity 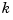, with 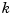the order of the spline 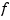. Failure to have such full multiplicity is particularly annoying when 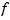is a spline curve, since the plot of that curve as produced by fnplt is then bound to start and finish at the origin, regardless of what the curve might otherwise do.

Further, since B-splines are zero outside their support, any function in B-form is zero outside the basic interval of its form. This is very much in contrast to a function in ppform whose values outside the basic interval of the form are given by the extension of its leftmost, respectively rightmost, polynomial piece.

fnmin

fnrfn