| Spline Toolbox | |
Syntax
Description
fnder(f,dorder)
dorderth derivative of the function whose description is contained in f. The default value of dorder is 1. For negative dorder, the particular |dorder|th indefinite integral is returned that vanishes |dorder|-fold at the left endpoint of the basic interval.
The output is of the same form as the input, i.e., they are both ppforms or both B-forms or both stforms. fnder does not work for rational splines; for them, use fntlr instead. fnder works for stforms only in a limited way: if the type is tp00, then dorder can be [1,0] or [0,1].
If the function in f is multivariate, say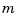 
-variate, then dorder must be given, and must be of length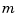 
.
Examples
If f is in ppform, or in B-form with its last knot of sufficiently high multiplicity, then, up to rounding errors, f and fnder(fnint(f)) are the same.
If f is in ppform and fa is the value of the function in f at the left end of its basic interval, then, up to rounding errors, f and fnint(fnder(f),fa) are the same, unless the function described by f has jump discontinuities.
If f contains the B-form of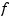 
, and 
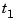is its left-most knot, then, up to rounding errors, fnint(fnder(f)) contains the B-form of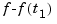 
. However, its left-most knot will have lost one multiplicity (if it had multiplicity > 1 to begin with). Also, its rightmost knot will have full multiplicity even if the rightmost knot for the B-form of 
in f doesn't.
Here is an illustration of this last fact. The spline in sp = spmak([0 0 1], 1) is, on its basic interval [0..1], the straight line that is 1 at 0 and 0 at 1. Now integrate its derivative: spdi = fnint(fnder(sp)). As you can check, the spline in spdi has the same basic interval, but, on that interval, it agrees with the straight line that is 0 at 0 and -1 at 1.
See the demos spalldem and ppalldem for examples.
Algorithm
For differentiation of either polynomial form, the derivatives are found in the piecewise-polynomial sense. This means that, in effect, each polynomial piece is differentiated separately, and jump discontinuities between polynomial pieces are ignored during differentiation.
For the B-form, the formulas [PGS; (X.10)] for differentiation are used.
For the stform, differentiation relies on knowing a formula for the relevant derivative of the basis function of the particular type.
See Also
fndir, fnint, fnplt, fnval, ppalldem, spalldem
| | fncmb | fndir | |