fnval (Spline Toolbox)

Evaluate a function

Syntax

values = fnval(f,x)
values = fnval(x,f)
values =  fnval(f,x,'l')
values =  fnval(x,f,'l')

Description

fnval(f,x) and fnval(x,f) both provide the matrix f(x), with 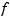the function whose description is contained in f. The output (and input) depends on whether 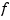is univariate or multivariate.

If the function in f is univariate, then the output is a matrix of size [d*m,n], with [m,n] the size of x and d the dimension of the target of 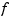(e.g., d is 2 if 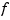maps into the plane).

If 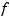has a jump discontinuity at x, then the value 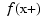, i.e., the limit from the right, is returned, except when x equals the right end of the basic interval of the form; for such x, the value 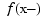, i.e., the limit from the left, is returned.

fnval(f,x,'l') and fnval(x,f,'l') also provide that matrix 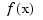, but treating 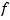as continuous from the left. This means that if 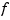has a jump discontinuity at x, then the value 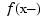, i.e., the limit from the left, is returned, except when x equals the left end of the basic interval; for such x, the value 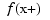is returned.

If the function is multivariate, then the above statements concerning continuity from the left and right apply coordinatewise. Further, if the function is, more precisely, m-variate for some m>1, then x must be either a list of m-vectors, i.e., of size [m,n], or a cell array {x1,...,xm} containing m vectors. In the first case, the output is of size [d*m,n] and contains the values of the function at the sites in x. In the second case, the output is of size [d,length(x1),...,length(xm)] (or of size [length(x1),...,length(xm)] in case d is 1), and contains the values of the function at the m-dimensional grid specified by x.

Examples

The statement fnval(csapi(x,y),xx) has the same effect as the statement csapi(x,y,xx).

Algorithm

For each entry of x, the relevant break- or knot-interval is determined and the relevant information assembled. Depending on whether f is in ppform or in B-form, nested multiplication or the B-spline recurrence (see, e.g., [PGS; X.(3)]) is then used vector-fashion for the simultaneous evaluation at all entries of x. Evaluation of a multivariate polynomial spline function takes full advantage of the tensor product structure.

Evaluation of a rational spline follows up evaluation of the corresponding vector-valued spline by division of all but its last component by its last component.

Evaluation of a function in stform makes essential use of stcol, and tries to keep the matrices involved to reasonable size.

See Also

fnbrk, ppmak, rsmak, spmak, stmak

fntlr fnzeros