ssv (Robust Control Toolbox)

Robust Control Toolbox

ssv

Compute the structured singular value (multivariable stability margin) Bode plot.

Syntax

[mu,logd] = ssv(a,b,c,d,w) 
[mu,logd] = ssv(a,b,c,d,w,k) 
[mu,logd] = ssv(a,b,c,d,w,k,opt)
[mu,logd] = ssv(ss,)

Description
ssv produces the row vector mu containing an upper bound on the structured singular value (SSV) of p x q a transfer function matrix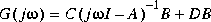

evaluated at frequency points in vector .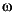

Several methods are included via the following input options:

opt -- options for method used in computing SSV:

'osborne' Osborne method

'psv' optimal diagonal scaled Perron eigenvalue (default)

'perron' Perron eigenvalue (if only mu output specified).

'muopt' Multiplier approach for pure real, pure complex and mixed real/complex uncertainties. If there exists real uncertainty, 'muopt' will be used (default for systems with mixed uncertainty).

k -- uncertainty block sizes (default: k=ones(q,2)); k can be an n x 1 or n x 2 matrix whose rows are the uncertainty block sizes for which the SSV is to be evaluated. If only the first column of k is given, then the uncertainty blocks are taken to be square, as if k(:,1) = k(:,2). If a 1 x 1 uncertainty block is real (say, the ith block), then you should assign

```
 k(i,:) = [-1, -1];
```

and set the input argument opt to 'muopt' to invoke the multiplier nonlinear programming algorithm to compute a less conservative SSV upper bound.

The output variables are:

mu -- the Bode plot of the SSV

logd -- the log Bode plot of the optimal diagonal scaling D(j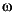). When the uncertainties are all complex, then D(j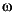) is purely real; this is always the case for the opt = 'psv' or opt = 'muopt' options. If opt = 'muopt' and the uncertainty is of the mixed real/complex type, logd in general will be complex and will contain the log Bode plot of the squareroots of the optimal multiplier scalings.

Algorithm
ssv performs its computation using either perron, psv, osborne, or muopt depending of the value of option. All of them can handle the irreducible special case where the standard algorithms fail. See the documentation for these functions for further details.

Examples
This example compares all the methods available in the Robust Control Toolbox for a less conservative multivariable stability margin prediction. The transfer function 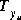seen by the real uncertainties is the one established in ACC Benchmark problem [4], which can be extracted from the demo accdemo.m. As shown in Figure 1-16, the multiplier solution provides the least conservative result, as compared to Perron and Osborne.

Figure 1-16: Comparison of Robust Analysis Methods.

References
[1] E. E. Osborne, "On Preconditioning of Matrices,'' J. of Assoc. of Computing Machinery, vol. 7, pp. 338-345, March 1960.

[2] M. G. Safonov, "Stability Margins for Diagonally Perturbed Multivariable Feedback Systems,'' IEE Proc., vol. 129, Part D, pp. 251-256, 1982.

[3] M. G. Safonov, and Peng-Hin Lee, "A Multiplier Method for Computing Real Multivariable Stability Margins,'' unpublished report, Electrical Eng. Dept., University of Southern Calif., Los Angeles, CA 90089-2563, July 1992; submitted to 1993 IFAC World Congress, Sydney, Australia.

[4] B. Wie and D. S. Bernstein, "A Benchmark Problem for Robust Controller Design," Proc. American Control Conf., San Diego, CA May 23-25, 1990; also Boston, MA, June 26-28, 1991.

sfl, sfr stabproj, slowfast