Robust Control Toolbox

Stable and antistable projection.

Slow and fast modes decomposition.

Syntax

• [a1,b1,c1,d1,a2,b2,c2,d2,m] = stabproj(a,b,c,d) 
  [a1,b1,c1,d1,a2,b2,c2,d2] = slowfast(a,b,c,d,cut) 
  [ss1,ss2,m] = stabproj(ss) 
  [ss1,ss2] = slowfast(ss,cut)
  

Description
stabproj computes the stable and antistable projections of a minimal realization G(s) such that

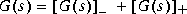
where 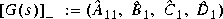denotes the stable part of G(s), and

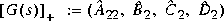denotes the antistable part. The variable m returns the number of stable eigenvalues of A.

Slowfast computes the slow and fast modes decompositions of a system G(s) such that

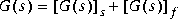
where 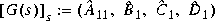denotes the slow part of G(s), and

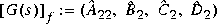denotes the fast part. The variable cut

denotes the index where the modes will be split.

Algorithm
Both stabproj and slowfast employ the algorithm in [1] as follows:

Find an unitary matrix V via the ordered Schur decomposition routines blksch or rschur such that

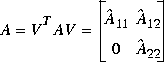
Based on the style of ordered Schur form, you can get a stable 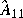and an antistable 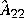for the case of stabproj; for the case of slowfast.

Finally solving the matrix equation for X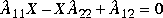

you get the state-space projections

where

and

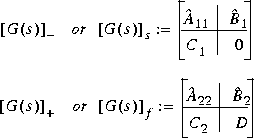
See Also
blkrsch, cschur, rschur, schur

References
[1] M. G. Safonov, E. A. Jonckheere, M. Verma and D. J. N. Limebeer, "Synthesis of Positive Real Multivariable Feedback Systems", Int. J. Control, vol. 45, no. 3, pp. 817-842, 1987.

ssv

tfm2ss