perron, psv (Robust Control Toolbox)

Robust Control Toolbox

perron, psv

Compute an upper bound on the structured singular value via the Perron eigenvector method.

Syntax

[mu] = perron(a) 
[mu] = perron(a,k) 
[mu,ascaled,logd] = psv(a)
[mu,ascaled,logd] = psv(a,k)

Description
perron produces the Perron eigenvalue for a given real or complex p by q matrix. This value serves as a scalar upper bound "mu" on the Structured Singular Value (SSV).

psv computes a tighter SSV upper bound mu via the formula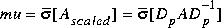

where D_p = diag(exp(logd)) is the Perron optimal diagonal scaling. In addition, psv returns the log magnitude of the optimal diagonal scaling logd in a column vector, and the scaled matrix 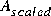is returned in ascaled.

The optional input k records the uncertainty block sizes with default value
k = ones(q, 2) corresponding to 1 by 1 uncertainty blocks. k can be an n by 1 or
n by 2 matrix whose rows are the uncertainty block sizes for which the SSV is to be evaluated. If only the first column of k is given, then each individual uncertainty block is taken to be square, as if k(:, 1) = k(:, 2).

Algorithm
The values of mu and logd are found by examining the eigenvalues and eigenvectors of the n by n nonnegative square matrix F formed from by A replacing each block of A (as defined by the partitioning k) by its greatest singular value. For any given positive square matrix (i.e., matrix with positive entries), there exists a positive real eigenvalue 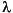_p of multiplicity one whose magnitude is greater than the real part of any other eigenvalue,

:

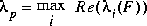This real eigenvalue 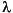_p is called the Perron eigenvalue of F, and its left and right eigenvectors, denoted as y_p and x_p respectively, are called Perron eigenvectors.

In 1982, Safonov [1] showed that the Perron eigenvalue is a good upper bound on the structured singular value µ, i.e.,

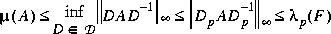
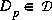is the Perron optimal scaling matrix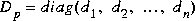

and

Moreover, the above inequalities become equalities when A = F so that, in the case in which A is a positive matrix and the uncertainty blocks are scalar, the Perron eigenvalue bound on µ is tight.

For reducible matrices the Perron optimal scaling matrix D_p can be singular, which would lead to numerical instability if corrective action were not taken. This problem is solved in psv (in the same fashion as it is in the function osborne) by very slightly perturbing the matrix F to a nearby irreducible matrix which has a slightly greater Perron eigenvalue. See osborne for further details and examples. Perturbation is not required with the perron function since D_p is not computed.

As compared to Osborne or nonlinear programming techniques, Perron eigenvector algorithms implemented by perron and psv require no iteration and so tend to be faster.

Examples
Several problems can be solved via the following psv commands, where most careless algorithms fail:

% An reducible case as compared to sigma 
A = eye(10); A(1,10) = 100000; 
[mu,Ascaled,logd] = psv(A); 
s1 = max(svd(A)); [s1, mu],
% Another reducible case as compared to sigma 
A = eye(8); 
A(1,3) = 100000; A(4,8) = 500000; 
[mu,Ascaled,logd] = psv(A); 
s1 = max(svd(A)); [s1, mu],

References
[1] M. G. Safonov, "Stability Margins for Diagonally Perturbed Multivariable Feedback Systems," IEE Proc., vol. 129, Part D, pp. 251-256, 1982.

osborne reig