| Robust Control Toolbox | |
Compute an upper bound on the structured singular value using multiplier approach.
Syntax
Description
muopt(A) produces the scalar upper bound mu on the structured singular value (ssv) of a pxq matrix A having n real or complex uncertainty blocks using the optimal multiplier method.
The optional input k records the uncertainty block sizes with default value
k = ones(p, 2). k can be an n by 1 or n by 2 matrix whose rows are the uncertainty block sizes for which the SSV is to be evaluated. If only the first column of k is given then each of the individual uncertainty blocks is taken to be square, as if k(:, 1) = k(:, 2). Real uncertainty (must be scalar) is indicated by multiplying the corresponding row of K by minus one, e.g., if the second uncertainty block is real then set K(2)=-1.
mu returns an upper bound on the real/complex structured singular value of A. The output ascaled returns the multiplier-scaled A-matrix
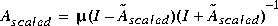
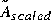= M½(µI - A)(µI + A)-1M-½* and M is the optimal diagonal generalized Popov multiplier scaling matrix. The output logm returns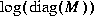 
, a complex vector of length p. The multiplier matrix M is related to the D,G-scales of [3] by 
.
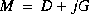x returns a normalized eigenvector associated with the smallest eigenvalue of the positive semidefinite matrix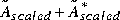 
.
Algorithm
muopt is based on the optimal generalized Popov multiplier theory of Safonov and Lee [1] and uses the computational algorithm of Fan and Nekooie [2]. The upper bound of µ returned is found as the solution to the optimization
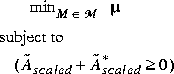
where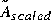 
= M½(µI - A)(µI + A)-1M-½* and M is the set of block diagonal generalized Popov multiplier for the uncertainty structure determined by k. This results in the returned value of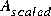 
satisfying 
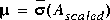. When µ=1, the Popov scaling matrix M is related to the D,G-scales of [3] by 
.
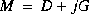Note that in the case in which all uncertainties are complex, the diagonal multiplier matrix M is real and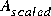 
becomes simply 
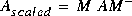. In this case the optimal µ is computed via the diagonally scaled singular value optimization 
.
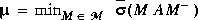Limitations
The algorithm in general produces a smaller upper bound on µ than perron, psv and osborne, but muopt requires significantly greater computation time than these other functions.
See Also
perron, psv, osborne, ssv
References
M. G. Safonov, and Peng-Hin Lee, "A Multiplier Method for Computing Real Multivariable Stability Margins,'' Proc. IFAC World Congress, Sydney, Australia, July 1993.
[2]
M.K.H. Fan and B. Nekooie, "An Interior Point Method for Solving Linear
Matrix Inequality Problems," SIAM J. Contr. and Optim., to appear.
[3]
M.K.H. Fan, A. Tits and J. Doyle, Robustness in the Present of Mixed
Parametric Uncertainty and Unmodelled Dynamics, IEEE Trans. on Autom.
Contr., vol. AC-36, no. 1, pp. 25-38, January 1991.
| mksys, vrsys, issystem | musyn | |