

| DSP Blockset |   |
Factor a matrix using singular value decomposition.
Library
Math Functions / Matrices and Linear Algebra / Matrix Factorizations
Description![]()
The Singular Value Decomposition block factors the M-by-N input matrix A such that
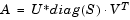
where U is an M-by-P matrix, V is an N-by-P matrix, S is a length-P vector, and P is defined as min(M,N).
When M = N, U and V are both M-by-M unitary matrices. When M > N, V is an N-by-N unitary matrix, and U is an M-by-N matrix whose columns are the first N columns of a unitary matrix. When N > M, U is an M-by-M unitary matrix, and V is an M-by-N matrix whose columns are the first N columns of a unitary matrix. In all cases, S is a 1-D vector of positive singular values having length P. The output is always sample-based.
Length-N row inputs are treated as length-N columns.
Note that the first (maximum) element of output S is equal to the 2-norm of the matrix A.
You can enable the U and V output ports by selecting the Output the singular vectors parameter.
Dialog Box
U and V output ports when selected.References
Golub, G. H., and C. F. Van Loan. Matrix Computations. 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.
Supported Data Types
To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.
See Also
| Autocorrelation LPC |
DSP Blockset |
| Cholesky Factorization |
DSP Blockset |
| LDL Factorization |
DSP Blockset |
| LU Inverse |
DSP Blockset |
| Pseudoinverse |
DSP Blockset |
| QR Factorization |
DSP Blockset |
| SVD Solver |
DSP Blockset |
svd |
MATLAB |
See Factoring Matrices for related information. Also see Matrix Factorizations for a list of all the blocks in the Matrix Factorizations library.
 | Sine Wave | Sort |  |