Sine Wave (DSP Blockset)

Generate a continuous or discrete sine wave.

Library

Description

The Sine Wave block generates a multichannel real or complex sinusoidal signal, with independent amplitude, frequency, and phase in each output channel. A real sinusoidal signal is generated when the Output complexity parameter is set to Real, and is defined by an expression of the type

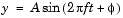
where A is specified by the Amplitude parameter, f is specified in hertz by the Frequency parameter, and 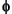is specified in radians by the Phase parameter. A complex exponential signal is generated when the Output complexity parameter is set to Complex, and is defined by an expression of the type

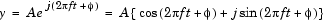
Sections of This Reference Page

Generating Multi-Channel Outputs

For both real and complex sinusoids, the Amplitude, Frequency, and Phase parameter values (A, f, and 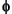) can be scalars or length-N vectors, where N is the desired number of channels in the output. If at least one of these parameters is specified as a length-N vector, scalar values specified for the other parameters are applied to every channel.

For example, to generate the three-channel output containing the real sinusoids below, set Output complexity to Real and the other parameters as follows:

Amplitude = [1 2 3]
Frequency = [1000 500 250]
Phase = [0 0 pi/2]

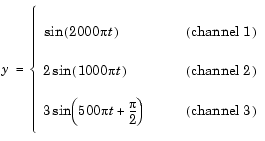
Output Sample Time and Samples Per Frame

In all discrete modes (see below), the block buffers the sampled sinusoids into frames of size M, where M is specified by the Samples per frame parameter. The output is a frame-based M-by-N matrix with frame period M*T_s, where T_s is specified by the Sample time parameter. For M=1, the output is sample-based.

Sample Mode

The Sample mode parameter specifies the block's sampling property, which can be Continuous or Discrete:

Continuous

In continuous mode, the sinusoid in the ith channel, y_i, is computed as a continuous function,

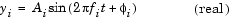
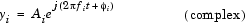
and the block's output is continuous. In this mode, the block's operation is the same as that of a Simulink Sine Wave block with Sample time set to 0. This mode offers high accuracy, but requires trigonometric function evaluations at each simulation step, which is computationally expensive. Additionally, because this method tracks absolute simulation time, a discontinuity will eventually occur when the time value reaches its maximum limit.

Note also that many blocks in the DSP Blockset do not accept continuous-time inputs.

Discrete

In discrete mode, the block's discrete-time output can be generated by directly evaluating the trigonometric function, by table look-up, or by a differential method. The three options are explained below.

Discrete Computational Methods

When Discrete is selected from the Sample mode parameter, the secondary Computation method parameter provides three options for generating the discrete sinusoid:

Trigonometric Fcn. The trigonometric function method computes the sinusoid in the ith channel, y_i, by sampling the continuous function

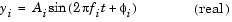
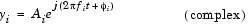
with a period of T_s, where T_s is specified by the Sample time parameter. This mode of operation shares the same benefits and liabilities as the Continuous sample mode described above.

If the period of every sinusoid in the output is evenly divisible by the sample period, meaning that 1/(f_iT_s) = k_i is an integer for every output y_i, then the sinusoidal output in the ith channel is a repeating sequence with a period of k_i samples. At each sample time, the block evaluates the sine function at the appropriate time value within the first cycle of the sinusoid. By constraining trigonometric evaluations to the first cycle of each sinusoid, the block avoids the imprecision of computing the sine of very large numbers, and eliminates the possibility of discontinuity during extended operations (when an absolute time variable might overflow). This method therefore avoids the memory demands of the table look-up method at the expense of many more floating-point operations.

Table Lookup. The table look-up method precomputes the unique samples of every output sinusoid at the start of the simulation, and recalls the samples from memory as needed. Because a table of finite length can only be constructed if all output sequences repeat, the method requires that the period of every sinusoid in the output be evenly divisible by the sample period. That is, 1/(f_iT_s) = k_i must be an integer value for every channel i = 1, 2, ..., N. When the Optimize table for parameter is set to Speed, the table constructed for each channel contains k_i elements. When the Optimize table for parameter is set to Memory, the table constructed for each channel contains k_i/4 elements.

For long output sequences, the table look-up method requires far fewer floating-point operations than any of the other methods, but may demand considerably more memory, especially for high sample rates (long tables). This is the recommended method for models that are intended to emulate or generate code for DSP hardware, and that therefore need to be optimized for execution speed.

Differential. The differential method uses an incremental (differential) algorithm rather than one based on absolute time. The algorithm computes the output samples based on the output values computed at the previous sample time (and precomputed update terms) by making use of the following identities.

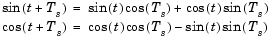
The update equations for the sinusoid in the ith channel, y_i, can therefore be written in matrix form (for real output) as

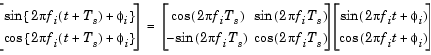
where T_s is specified by the Sample time parameter. Since T_s is constant, the right-hand matrix is a constant and can be computed once at the start of the simulation. The value of A_isin[2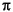f_i(t+T_s)+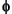_i] is then computed from the values of sin(2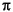f_it+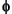_i) and cos(2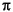f_it+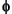_i) by a simple matrix multiplication at each time step.

This mode offers reduced computational load, but is subject to drift over time due to cumulative quantization error. Because the method is not contingent on an absolute time value, there is no danger of discontinuity during extended operations (when an absolute time variable might overflow).

Examples

The dspsinecomp demo provides a comparison of all the available sine generation methods.

Dialog Box

Amplitude: A length-N vector containing the amplitudes of the sine waves in each of N output channels, or a scalar to be applied to all N channels. The vector length must be the same as that specified for the Frequency and Phase parameters. Tunable (when Computation method is not set to Table lookup); when the amplitude values can be altered while a simulation is running, but the vector length must remain the same.
Frequency: A length-N vector containing frequencies, in rad/s, of the sine waves in each of N output channels, or a scalar to be applied to all N channels. The vector length must be the same as that specified for the Amplitude and Phase parameters. You can specify positive, zero, or negative frequencies. Tunable (when Computation method is not set to Table lookup); the frequency values can be altered while a simulation is running, but the vector length must remain the same. Not tunable in the Simulink external mode when using the differential method.
Phase offset: A length-N vector containing the phase offsets, in radians, of the sine waves in each of N output channels, or a scalar to be applied to all N channels. The vector length must be the same as that specified for the Amplitude and Frequency parameters. Tunable (when Computation method is not set to Table lookup); the phase values can be altered while a simulation is running, but the vector length must remain the same. Not tunable in the Simulink external mode when using the differential method.
Sample mode: The block's sampling behavior, Continuous or Discrete.
Output complexity: The type of waveform to generate: Real specifies a real sine wave, Complex specifies a complex exponential. Tunable.
Computation method: The method by which discrete-time sinusoids are generated: Trigonometric fcn, Table lookup, or Differential. This parameter is disabled when Continuous is selected from the Sample mode parameter. For details, see Discrete Computational Methods.
Optimize table for: Optimizes the table of sine values for Speed or Memory (this parameter is only visible when the Computation method parameter is set to Table lookup). When optimized for speed, the table contains k elements, and when optimized for memory, the table contains k/4 elements, where k is the number of input samples in one full period of the sine wave.
Sample time: The period with which the sine wave is sampled, T_s. The block's output frame period is M*T_s, where M is specified by the Samples per frame parameter. This parameter is disabled when Continuous is selected from the Sample mode parameter.
Samples per frame: The number of consecutive samples from each sinusoid to buffer into the output frame, M. This parameter is disabled when Continuous is selected from the Sample mode parameter.
Show additional parameters: If selected, additional parameters specific to implementation of the block become visible as shown.
Output data type: Specify the output data type in out of the following ways:

Choose one of the built-in data types from the drop-down list.
Choose Fixed-point to specify the output data type and scaling in the Word length, Set fractional bits in output to, and Number of fractional bits in output parameters.
Choose User-defined to specify the output data type and scaling in the User-defined data type, Set fractional bits in output to, and Number of fractional bits in output parameters.
Choose Inherit via back propagation to set the output data type and scaling to match the next block downstream.

Word length: Specify the word length, in bits, of the fixed-point output data type. This parameter is only visible if Fixed-point is selected for the Output data type parameter.
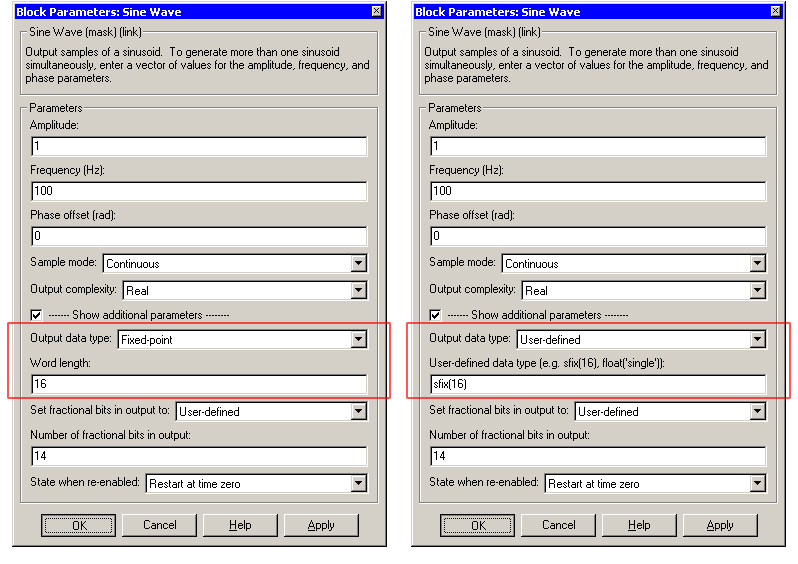
User-defined data type: Specify any built-in or fixed-point data type. You can specify fixed-point data types using the sfix, ufix, sint, uint, sfrac, and ufrac functions from the Fixed-Point Blockset. This parameter is only visible if User-defined is selected for the Output data type parameter.
Set fractional bits in output to: Specify the scaling of the fixed-point output by either of the following two methods:

Choose Best precision to have the output scaling automatically set such that the output signal has the best possible precision.
Choose User-defined to specify the output scaling in the Number of fractional bits in output parameter.
This parameter is only visible if Fixed-point or User-defined is selected for the Output data type parameter, and if the specified output data type is a fixed-point data type.

Number of fractional bits in output: For fixed-point output data types, specify the number of fractional bits, or bits to the right of the binary point. This parameter is only visible if Fixed-point or User-defined is selected for the Output data type parameter, and if User-defined is selected for the Set fractional bits in output to parameter.
State when re-enabled: The behavior of the block when a disabled subsystem containing it is reenabled. The block can either reset itself to its starting state (Restart at time zero), or resume generating the sinusoid based on the current simulation time (Catch up to simulation time). This parameter is disabled when Continuous is selected from the Sample mode parameter.

Supported Data Types

Double-precision floating point
Single-precision floating point
Fixed-point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

Chirp
DSP Blockset

Complex Exponential
DSP Blockset

Signal From Workspace
DSP Blockset

Signal Generator
Simulink

Sine Wave
Simulink

sin
MATLAB

Chirp	DSP Blockset
Complex Exponential	DSP Blockset
Signal From Workspace	DSP Blockset
Signal Generator	Simulink
Sine Wave	Simulink
`sin`	MATLAB

Also see the following topics:

Creating Signals Using Signal Generator Blocks -- How to use this and other blocks to generate signals
DSP Sources -- List of all blocks in the DSP Sources library

Signal To Workspace Singular Value Decomposition