DSP Blockset

Downsample

Resample an input at a lower rate by deleting samples.

Library

Signal Operations

Description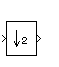

The Downsample block resamples each channel of the M_i-by-N input at a rate K times lower than the input sample rate by discarding K-1 consecutive samples following each sample passed through to the output. The integer K is specified by the Downsample factor parameter.

The Sample offset parameter delays the output samples by an integer number of sample periods, D, where 0 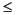D < (K-1), so that any of the K possible output phases can be selected. For example, when you downsample the sequence 1, 2, 3, ... by a factor of 4, you can select from the following four phases.

Input Sequence	Sample Offset, D	Output Sequence (K=4)
1,2,3,...	0	0,1,5,9,13,17,21,25,...
1,2,3,...	1	0,2,6,10,14,18,22,26,...
1,2,3,...	2	0,3,7,11,15,19,23,27,...
1,2,3,...	3	0,4,8,12,16,20,24,28,...

The initial zero in each output sequence above is a result of the default zero Initial condition parameter setting for this example. See Latency for more on the Initial condition parameter.

Sample-Based Operation

When the input is sample-based, the block treats each of the M*N matrix elements as an independent channel, and downsamples each channel over time. The input and output sizes are identical.

The Sample-based mode parameter determines how the block represents the new rate at the output. There are two available options:

• Allow multirate

• When Allow multirate is selected, the sample period of the sample-based output is K times longer than the input sample period (T_so = KT_si). The block is therefore multirate.

• Enforce single rate

• When Enforce single rate is selected, the block forces the output sample rate to match the input sample rate (T_so = T_si) by repeating every Kth input sample K times at the output. The block is therefore single-rate. (The block's operation when Enforce single rate is selected is similar to the operation of a Sample and Hold block with a repeating trigger event of period KT_si.)

The setting of the Frame-based mode popup menu does not affect sample-based inputs.

Frame-Based Inputs

When the input is frame-based, the block treats each of the N input columns as a frame containing M_i sequential time samples from an independent channel. The block downsamples each channel independently by discarding K-1 rows of the input matrix following each row that it passes through to the output.

The Frame-based mode parameter determines how the block adjusts the rate at the output to accommodate the reduced number of samples. There are two available options:

• Maintain input frame size

• The block generates the output at the slower (downsampled) rate by using a proportionally longer frame period at the output port than at the input port. For downsampling by a factor of K, the output frame period is K times longer than the input frame period (T_fo = KT_fi), but the input and output frame sizes are equal.

  The model below shows a single-channel input with a frame period of 1 second being downsampled by a factor of 4 to a frame period of 4 seconds. The input and output frame sizes are identical.

  

• Maintain input frame rate

• The block generates the output at the slower (downsampled) rate by using a proportionally smaller frame size than the input. For downsampling by a factor of K, the output frame size is K times smaller than the input frame size (M_o = M_i/K), but the input and output frame rates are equal.

  The model below shows a single-channel input of frame size 64 being downsampled by a factor of 4 to a frame size of 16. The input and output frame rates are identical.

  

The setting of the Sample-based mode popup menu does not affect frame-based inputs.

Latency

Zero Latency.   The Downsample block has zero tasking latency for the special combinations of input signal sampling and parameter settings shown in the table below. In all of these cases the block has single-rate operation.

Input Sampling	Parameter Settings
Sample-based	Downsample factor parameter, K, is 1, or Enforce single rate is selected (with D=0)
Frame-based	Downsample factor parameter, K, is 1, or Maintain input frame rate is selected

Zero tasking latency means that the block propagates input sample D+1 (received at t=0) as the first output sample, followed by input sample D+1+K, input sample D+1+2K, and so on. The Initial condition parameter value is not used.

Nonzero Latency.   The Downsample block is multirate for most settings other than those in the above table. The amount of latency for multirate operation depends on input signal sampling and the Simulink tasking mode, as shown in the table below.

Multirate...	Sample-Based Latency	Frame-Based Latency
Single-tasking	None, for D=0 One sample, for D>0	One frame (Mi samples)
Multitasking	One sample	One frame (Mi samples)

The only case of nonzero single-rate latency occurs in sample-based mode, when Enforce single rate is selected with D > 0. The latency in this case is one sample.

In all cases of one-sample latency, the initial condition for each channel appears as the first output sample. Input sample D+1 appears as the second output sample for each channel, followed by input sample D+1+K, input sample D+1+2K, and so on. The Initial condition parameter can be an M_i-by-N matrix containing one value for each channel, or a scalar to be applied to all signal channels.

In all cases of one-frame latency, the M_i rows of the initial condition matrix appear in sequence as the first M_i output rows. Input sample D+1 (i.e, row D+1 of the input matrix) appears in the output as sample M_i+1, followed by input sample D+1+K, input sample D+1+2K, and so on. The Initial condition value can be an M_i-by-N matrix, or a scalar to be repeated across all elements of the M_i-by-N matrix. See the example below for an illustration of this case.

See Excess Algorithmic Delay (Tasking Latency) and "The Simulation Parameters Dialog Box" in the Simulink documentation for more information about block rates and the Simulink tasking modes.

Example

Construct the frame-based model shown below.

Adjust the block parameters as follows:

• Configure the Signal From Workspace block to generate a two-channel signal with frame size of 4 and sample period of 0.25 second. This represents an output frame period of 1 second (0.25*4). The first channel should contain the positive ramp signal 1, 2, ..., 100, and the second channel should contain the negative ramp signal -1, -2, ..., -100. The settings are:
• Signal = [(1:100)' (-1:-1:-100)']
• Sample time = 0.25
• Samples per frame = 4
• Configure the Downsample block to downsample the two-channel input by decreasing the output frame rate by a factor of 2 relative to the input frame rate. Set a sample offset of 1, and a 4-by-2 initial condition matrix of

• Downsample factor = 2
• Sample offset = 1
• Initial condition = [11 -11;12 -12;13 -13;14 -14]
• Frame-based mode = Maintain input frame size

• Configure the Probe blocks by clearing the Probe width and Probe complex signal check boxes (if desired).

This model is multirate because there are at least two distinct frame rates, as shown by the two Probe blocks. To run this model in the Simulink multitasking mode, select Fixed-step and discrete from the Type controls in the Solver panel of the Simulation Parameters dialog box, and select MultiTasking from the Mode parameter. Additionally, set the Stop time to 30.

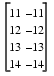
Run the model and look at the output, yout. The first few samples of each channel are shown below.

• yout =
      11   -11
      12   -12
      13   -13
      14   -14
       2    -2
       4    -4
       6    -6
       8    -8
      10   -10
      12   -12
      14   -14
  

Since we ran this frame-based multirate model in multitasking mode, the first row of the initial condition matrix appears as the first output sample, followed by the other three initial condition rows. The second row of the first input matrix (i.e., row D+1, where D is the Sample offset) appears in the output as sample 5 (i.e., sample M_i+1, where M_i is the input frame size).

Dialog Box

Downsample factor

The integer factor, K, by which to decrease the input sample rate.

Sample offset

The sample offset, D, which must be an integer in the range [0, K-1].

Initial condition

The value with which the block is initialized for cases of nonzero latency; a scalar or matrix.

Sample-based mode

The method by which to implement downsampling for sample-based inputs: Allow multirate (i.e, decrease the output sample rate), or Force single-rate (i.e., force the output sample rate to match the input sample rate by repeating every Kth input sample K times at the output).

Frame-based mode

The method by which to implement downsampling for frame-based inputs: Maintain input frame size (i.e., decrease the frame rate), or Maintain input frame rate (i.e., decrease the frame size).

Supported Data Types

• Double-precision floating point
• Single-precision floating point
• Fixed-point
• Custom data types
• Boolean
• 8-, 16-, and 32-bit signed integers
• 8-, 16-, and 32-bit unsigned integers

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

FIR Decimation	DSP Blockset
FIR Rate Conversion	DSP Blockset
Repeat	DSP Blockset
Sample and Hold	DSP Blockset
Upsample	DSP Blockset

Also see Signal Operations for a list of all the blocks in the Signal Operations library.

Discrete Impulse

DSP Constant