DSP Blockset

FIR Decimation

Filter and downsample an input signal.

Library

Filtering / Multirate Filters

Description

The FIR Decimation block resamples the discrete-time input at a rate K times slower than the input sample rate, where the integer K is specified by the Decimation factor parameter. This process consists of two steps:

• The block filters the input data using a direct-form II transpose FIR filter.
• The block downsamples the filtered data to a lower rate by discarding K-1 consecutive samples following every sample retained.

The FIR Decimation block implements the above FIR filtering and downsampling steps together using a polyphase filter structure, which is more efficient than straightforward filter-then-decimate algorithms. The output of the decimator is the first phase of the polyphase filter.

The FIR filter coefficients parameter specifies the numerator coefficients of the FIR filter transfer function H(z).

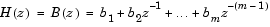
The length-m coefficient vector, [b(1) b(2) ... b(m)], can be generated by one of the filter design functions in the Signal Processing Toolbox, such as the fir1 function used in the example below. The filter should be lowpass with normalized cutoff frequency no greater than 1/K. All filter states are internally initialized to zero.

Sample-Based Operation

An M-by-N sample-based matrix input is treated as M*N independent channels, and the block decimates each channel over time. The output sample period is K times longer than the input sample period (T_so = KT_si), and the input and output sizes are identical.

Frame-Based Operation

An M_i-by-N frame-based matrix input is treated as N independent channels, and the block decimates each channel over time. The Framing parameter determines how the block adjusts the rate at the output to accommodate the reduced number of samples. There are two available options:

• Maintain input frame size

• The block generates the output at the slower (decimated) rate by using a proportionally longer frame period at the output port than at the input port. For decimation by a factor of K, the output frame period is K times longer than the input frame period (T_fo = KT_fi), but the input and output frame sizes are equal.

  The example below shows a single-channel input with a frame period of 1 second (Sample time = 1/64 and Samples per frame = 64 in the Signal From Workspace block) being decimated by a factor of 4 to a frame period of 4 seconds. The input and output frame sizes are identical.

  

• Maintain input frame rate

• The block generates the output at the slower (decimated) rate by using a proportionally smaller frame size than the input. For decimation by a factor of K, the output frame size is K times smaller than the input frame size (M_o = M_i/K), but the input and output frame rates are equal. The input frame size, M_i, must be a multiple of the decimation factor, K.

  The example below shows a single-channel input of frame size 64 being decimated by a factor of 4 to a frame size of 16. The block's input and output frame rates are identical.

  

Latency

Zero Latency.   The FIR Decimation block has zero tasking latency for all single-rate operations. The block is single-rate for the particular combinations of sampling mode and parameter settings shown in the table below.

Sampling Mode	Parameter Settings
Sample-based	Decimation factor parameter, K, is 1.
Frame-based	Decimation factor parameter, K, is 1, or Framing parameter is Maintain input frame rate.

Note that in sample-based mode, single-rate operation occurs only in the trivial case of factor-of-1 decimation.

The block also has zero latency for sample-based multirate operations in the Simulink single-tasking mode. Zero tasking latency means that the block propagates the first filtered input sample (received at t=0) as the first output sample, followed by filtered input samples K+1, 2K+1, and so on.

Nonzero Latency.   The FIR Decimation block is multirate for all settings other than those in the above table. The amount of latency for multirate operation depends on the Simulink tasking mode and the block's sampling mode, as shown in the table below.

Multirate...	Sample-Based Latency	Frame-Based Latency
Single-tasking	None	One frame (Mi samples)
Multitasking	One sample	One frame (Mi samples)

In cases of one-sample latency, a zero initial condition appears as the first output sample in each channel. The first filtered input sample appears as the second output sample, followed by filtered input samples K+1, 2K+1, and so on.

In cases of one-frame latency, the first M_i output rows contain zeros, where M_i is the input frame size. The first filtered input sample (first filtered row of the input matrix) appears in the output as sample M_i+1, followed by filtered input samples K+1, 2K+1, and so on. See the example below for an illustration of this case.

See Excess Algorithmic Delay (Tasking Latency) and "The Simulation Parameters Dialog Box" in the Simulink documentation for more information about block rates and the Simulink tasking modes.

Examples

Example 1

Construct the frame-based model shown below.

Adjust the block parameters as follows:

• Configure the Signal From Workspace block to generate a two-channel signal with frame size of 4 and sample period of 0.25. This represents an output frame period of 1 (0.25*4). The first channel should contain the positive ramp signal 1, 2, ..., 100, and the second channel should contain the negative ramp signal -1, -2, ..., -100.
• Signal = [(1:100)' (-1:-1:-100)']
• Sample time = 0.25
• Samples per frame = 4
• Configure the FIR Decimation block to decimate the two-channel input by decreasing the output frame rate by a factor of 2 relative to the input frame rate. Use a third-order filter with normalized cutoff frequency, f_n0, of 0.25. (Note that f_n0 satisfies f_n01/K.)
• FIR filter coefficients = fir1(3,0.25)
• Downsample factor = 2
• Framing = Maintain input frame size

• The filter coefficient vector generated by fir1(3,0.25) is

  • [0.0386 0.4614 0.4614 0.0386]
    

  or, equivalently,

• Configure the Probe blocks by clearing the Probe width, Probe complex signal, and Probe signal dimensions check boxes (if desired).

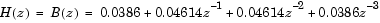
This model is multirate because there are at least two distinct sample rates, as shown by the two Probe blocks. To run this model in the Simulink multitasking mode, select Fixed-step and discrete from the Type controls in the Solver panel of the Simulation Parameters dialog box, and select MultiTasking from the Mode parameter. Also set the Stop time to 30.

Run the model and look at the output, yout. The first few samples of each channel are shown below.

• yout =
           0         0
           0         0
           0         0
           0         0
      0.0386   -0.0386
      1.5000   -1.5000
      3.5000   -3.5000
      5.5000   -5.5000
      7.5000   -7.5000
      9.5000   -9.5000
     11.5000  -11.5000
  

Since we ran this frame-based multirate model in multitasking mode, the first four (M_i) output rows are zero. The first filtered input matrix row appears in the output as sample 5 (i.e., sample M_i+1).

Example 2

The dspmrf_menu demo illustrates the use of the FIR Decimation block in a number of multistage multirate filters.

Dialog Box

FIR filter coefficients

The lowpass FIR filter coefficients, in descending powers of z.

Decimation factor

The integer factor, K, by which to decrease the sample rate of the input sequence.

Framing

For frame-based operation, the method by which to implement the decimation; reduce the output frame rate, or reduce the output frame size.

Supported Data Types

• Double-precision floating point
• Single-precision floating point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

Downsample	DSP Blockset
FIR Interpolation	DSP Blockset
FIR Rate Conversion	DSP Blockset
decimate	Signal Processing Toolbox
fir1	Signal Processing Toolbox
fir2	Signal Processing Toolbox
firls	Signal Processing Toolbox
remez	Signal Processing Toolbox

See the following sections for related information:

• Converting Sample Rates and Frame Rates
• Multirate Filters
• Filtering -- List of all DSP Blockset filtering blocks

Filter Realization Wizard

FIR Interpolation