| Curve Fitting Toolbox | |
Library Models
The parametric library models provided by the Curve Fitting Toolbox are described below.
Exponentials
The toolbox provides a one-term and a two-term exponential model.
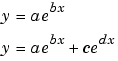
Exponentials are often used when the rate of change of a quantity is proportional to the initial amount of the quantity. If the coefficient associated with e is negative, y represents exponential decay. If the coefficient is positive, y represents exponential growth.
For example, a single radioactive decay mode of a nuclide is described by a one-term exponential. a is interpreted as the initial number of nuclei, b is the decay constant, x is time, and y is the number of remaining nuclei after a specific amount of time passes. If two decay modes exist, then you must use the two-term exponential model. For each additional decay mode, you add another exponential term to the model.
Examples of exponential growth include contagious diseases for which a cure is unavailable, and biological populations whose growth is uninhibited by predation, environmental factors, and so on.
Fourier Series
The Fourier series is a sum of sine and cosine functions that is used to describe a periodic signal. It is represented in either the trigonometric form or the exponential form. The toolbox provides the trigonometric Fourier series form shown below,
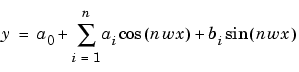
where a0 models any DC offset in the signal and is associated with the i = 0 cosine term, w is the fundamental frequency of the signal, n is the number of terms (harmonics) in the series, and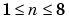 
.
For more information about the Fourier series, refer to Fourier Analysis and the Fast Fourier Transform in the MATLAB documentation. For an example that fits the ENSO data to a custom Fourier series model, refer to General Equation: Fourier Series Fit.
Gaussian
The Gaussian model is used for fitting peaks, and is given by the equation
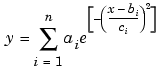
where a is the amplitude, b is the centroid (location), c is related to the peak width, n is the number of peaks to fit, and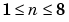 
.
Gaussian peaks are encountered in many areas of science and engineering. For example, line emission spectra and chemical concentration assays can be described by Gaussian peaks. For an example that fits two Gaussian peaks and an exponential background, refer to General Equation: Gaussian Fit with Exponential Background.
Polynomials
Polynomial models are given by
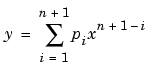
where n + 1 is the order of the polynomial, n is the degree of the polynomial, and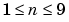 
. The order gives the number of coefficients to be fit, and the degree gives the highest power of the predictor variable.
In this guide, polynomials are described in terms of their degree. For example, a third-degree (cubic) polynomial is given by
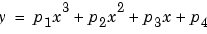
Polynomials are often used when a simple empirical model is required. The model can be used for interpolation or extrapolation, or it can be used to characterize data using a global fit. For example, the temperature-to-voltage conversion for a Type J thermocouple in the 0o to 760o temperature range is described by a seventh-degree polynomial.
| Note If you do not require a global parametric fit and want to maximize the flexibility of the fit, piecewise polynomials might provide the best approach. Refer to Nonparametric Fitting for more information. |
The main advantages of polynomial fits include reasonable flexibility for data that is not too complicated, and they are linear, which means the fitting process is simple. The main disadvantage is that high-degree fits can become unstable. Additionally, polynomials of any degree can provide a good fit within the data range, but can diverge wildly outside that range. Therefore, you should exercise caution when extrapolating with polynomials. Refer to Determining the Best Fit for examples of good and poor polynomial fits to census data.
Note that when you fit with high-degree polynomials, the fitting procedure uses the predictor values as the basis for a matrix with very large values, which can result in scaling problems. To deal with this, you should normalize the data by centering it at zero mean and scaling it to unit standard deviation. You normalize data by selecting the Center and scale X data check box on the Fitting GUI.
Power Series
The toolbox provides a one-term and a two-term power series model.
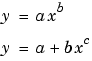
Power series models are used to describe a variety of data. For example, the rate at which reactants are consumed in a chemical reaction is generally proportional to the concentration of the reactant raised to some power.
Rationals
Rational models are defined as ratios of polynomials and are given by
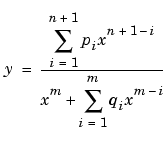
where n is the degree of the numerator polynomial and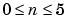 
, while m is the degree of the denominator polynomial and 
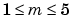. Note that the coefficient associated with 
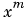is always 1. This makes the numerator and denominator unique when the polynomial degrees are the same.
In this guide, rationals are described in terms of the degree of the numerator/the degree of the denominator. For example, a quadratic/cubic rational equation is given by
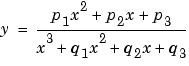
Like polynomials, rationals are often used when a simple empirical model is required. The main advantage of rationals is their flexibility with data that has complicated structure. The main disadvantage is that they become unstable when the denominator is around zero. For an example that uses rational polynomials of various degrees, refer to Example: Rational Fit.
Sum of Sines
The sum of sines model is used for fitting periodic functions, and is given by the equation
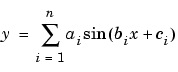
where a is the amplitude, b is the frequency, and c is the phase constant for each sine wave term. n is the number of terms in the series and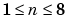 
. This equation is closely related to the Fourier series described previously. The main difference is that the sum of sines equation includes the phase constant, and does not include a DC offset term.
Weibull Distribution
The Weibull distribution is widely used in reliability and life (failure rate) data analysis. The toolbox provides the two-parameter Weibull distribution
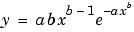
where a is the scale parameter and b is the shape parameter. Note that there is also a three-parameter Weibull distribution with x replaced by x - c where c is the location parameter. Additionally, there is a one-parameter Weibull distribution where the shape parameter is fixed and only the scale parameter is fitted. To use these distributions, you must create a custom equation.
Note that the Curve Fitting Toolbox does not fit Weibull probability distributions to a sample of data. Instead, it fits curves to response and predictor data such that the curve has the same shape as a Weibull distribution.
| | The Least Squares Fitting Method | Custom Equations | |