| Curve Fitting Toolbox | |
Parametric Fitting
Parametric fitting involves finding coefficients (parameters) for one or more models that you fit to data. The data is assumed to be statistical in nature and is divided into two components: a deterministic component and a random component.
The deterministic component is given by the fit and the random component is often described as error associated with the data.
The fit is given by a model that is a function of the independent (predictor) variable and one or more coefficients. The error represents random variations in the data that follow a specific probability distribution (usually Gaussian). The variations can come from many different sources, but are always present at some level when you are dealing with measured data. Systematic variations can also exist, but they can be difficult to quantify.
The fitted coefficients often have physical significance. For example, suppose you have collected data that corresponds to a single decay mode of a radioactive nuclide, and you want to find the half-life (T1/2) of the decay. The law of radioactive decay states that the activity of a radioactive substance decays exponentially in time. Therefore, the model to use in the fit is given by
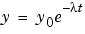
where y0 is the number of nuclei at time t = 0, and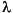 
is the decay constant. Therefore, the data can be described by
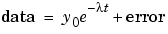
Both y0 and 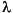are coefficients determined by the fit. Because T1/2 = ln(2)/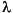, the fitted value of the decay constant yields the half-life. However, because the data contains some error, the deterministic component of the equation cannot completely describe the variability in the data. Therefore, the coefficients and half-life calculation will have some uncertainty associated with them. If the uncertainty is acceptable, then you are done fitting the data. If the uncertainty is not acceptable, then you might have to take steps to reduce the error and repeat the data collection process.
| | The Fitting Process | Basic Assumptions About the Error | |