Signal Processing Toolbox

stmcb

Steiglitz-McBride反復法を使った線形モデル

表示

[b,a] = stmcb(x,nb,na)
[b,a] = stmcb(x,u,nb,na)
[b,a] = stmcb(x,nb,na,niter)
[b,a] = stmcb(x,u,nb,na,niter)
[b,a] = stmcb(x,nb,na,niter,ai)
[b,a] = stmcb(x,u,nb,na,niter,ai)

詳細

Steiglitz-McBride反復法は、設定された時間領域インパルス応答をもつIIRフィルタを求めるアルゴリズムです。これは、フィルタ設計とシステム同定(パラメトリックモデリング)に適用できます。

[b,a] = stmcb(x,nb,na) は、近似的にインパルス応答xをもつシステム b(z)/a(z)の係数を求めます。ここで、nbは零点の数、naは極の数です。

[b,a] = stmcb(x,u,nb,na) は、入力としてuを与え、出力としてxをもつシステムのシステム係数bおよびaを求めます。x とuは、同じ長さでなければなりません。

[b,a] = stmcb(x,nb,na,niter) および

[b,a] = stmcb(x,u,nb,na,niter) は、niter回反復します。niterのデフォルトは5です。

[b,a] = stmcb(x,nb,na,niter,ai) および

[b,a] = stmcb(x,u,nb,na,niter,ai) は、分母係数の初期推定値としてベクトルaiを使用します。aiを設定しないと、stmcbは[b,ai] = prony(x,0,na)の出力引数をベクトルaiとして使用します。

stmcbは、IIRフィルタの係数を長さnb+1とna+1の行ベクトルbおよびaに出力します。フィルタ係数は、zの次数の降順で順序付けられます。

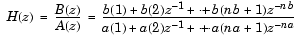
例題

Butterworthフィルタのインパルス応答を、より低次のシステムに近似させます。

[b,a] = butter(6,0.2);
h = filter(b,a,[1 zeros(1,100)]);
freqz(b,a,128)


[bb,aa] = stmcb(h,4,4);
freqz(bb,aa,128)

アルゴリズム

stmcbは、b(z)/a(z)のインパルス応答x'と入力信号xとの間の二乗和誤差を最小化します。

stmcbは、つぎの2つのステップを繰り返します。

1. 1/a(z)を使って、xおよびuをフィルタ処理します。
2. \を使って、b とa の連立1次方程式を解きます。

stmcbは、このプロセスをniter回繰り返します。bおよびaの係数がniter回の反復より前に収束したかどうかについてのチェックは行われません。

診断

xとuの長さが異なる場合、stmcbは、つぎのエラーメッセージを表示します。

X and U must have same length.

参考

levinson	Levinson-Durbin再帰法
lpc	線形予測係数
aryule	Yule-Walker法を使ったARモデルパラメータの推定
prony	Prony法を使った時間領域IIRフィルタ設計

参考文献

[1] Steiglitz, K., and L.E. McBride, "A Technique for the Identification of Linear Systems," IEEE Trans. Automatic Control, Vol. AC-10 (1965), pp. 461-464.

[2] Ljung, L., System Identification: Theory for the User, Prentice-Hall, Englewood Cliffs, NJ, 1987, p. 297.

ss2zp

strips