| Signal Processing Toolbox | |
表示
r=rlevinson(a,efinal) [r,u]=rlevinson(a,efinal) [r,u,k]=rlevinson(a,efinal) [r,u,k,e]=rlevinson(a,efinal)
詳細
逆Levinson-Durbin帰納法は、rに対するつぎの対称Toeplitz線形連立方程式を解くために、下降演算アルゴリズムを実行します。ここで、r = [r(1) L r(p+1)] で、r(i)* は、r(i)の複素共役を定義します。
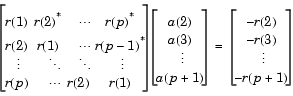
r は、ベクトル = rlevinson(a,efinal)
aを与えて、rに対する上のシステムを解きます。ここで、 a = [1 a(2) L a(p+1)]です。線形予測のアプリケーションにおいて、rは、入力の自己相関列で、予測誤差フィルタを表わします。ここで、r(1)はゼロラグの要素です。つぎの図は、このタイプの典型的なフィルタを示しています。ここで、H(z) は最適線形予測子で、 x(n) は入力信号、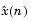
は予測信号、e(n)は予測誤差です。
入力ベクトルaは、zに関して降順に並べたこの予測誤差フィルタの多項式係数を表わします。
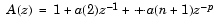
フィルタは、正しい自己相関列を作成するために最小位相でなければなりません。efinal は、スカラの予測誤差のパワーで、予測誤差信号の分散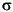
2(e)と等しくなります。
[r,u] は， UDU*分解から上三角行列Uを出力します。 = rlevinson(a,efinal)
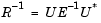
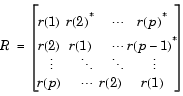
で、 Eは、出力eに出力される対角行列要素です。この分解は、自己相関行列の逆行列R-1の有効な計算方法です。
出力行列uは、逆Levinson-Durbin帰納法の各繰り返しからの予測多項式aを含んでいます。
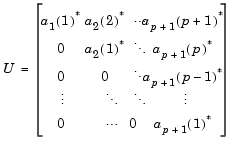
ここで、 ai(j) は、i次の予測多項式(たとえば、iステップの計算)のj番目の係数です。たとえば、5次の予測多項式は、つぎのようになります。
a5 = u(5:-1:1,5)'
u(p+1:-1:1,p+1)'は、入力多項式係数ベクトル aであることに注意してください。
[r,u,k] は、反射係数を含む長さ(p+1)のベクトル = rlevinson(a,efinal)
kを出力します。反射係数は、uの最初の行に共役なものを設定しています。
k = conj(u(1,2:end))
[r,u,k,e] は、逆Levinson-Durbin帰納法の各繰り返しからの予測誤差を含む長さ(p+1)のベクトルを出力します。すなわち、 = rlevinson(a,efinal)
e(1) は、1次モデルに対する予測誤差、e(2)は2次モデルに対する予測誤差というようになります。
これらの予測誤差は、R-1のUDU* 分解の中の行列Eの対角要素から構成されます。
.
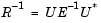参考
|
Levinson-Durbin再帰法 |
|
線形予測係数 |
|
Prony法を使った時間領域IIRフィルタ設計 |
|
Steiglitz-McBride反復法を使った線形モデル |
参考文献
[1] Kay, S.M., Modern Spectral Estimation: Theory and Application, Prentice-Hall, Englewood Cliffs, NJ, 1988.
| | residuez | rooteig | |