Signal Processing Toolbox

poly2rc

予測多項式を反射係数に変換

表示

k = poly2rc(a)
[k,r0] = poly2rc(a,efinal)

詳細

k = poly2rc(a) は、AR予測フィルタ多項式をARラティス構造の対応する反射係数に変換します。aは実数でなければなりません。a(1)は0をとることはできません。a(1)が1でない場合、poly2rcは、a(1)で予測多項式を正規化します。kは、大きさ(length(a)-1)の行ベクトルです。

[k,r0] = poly2rc(a,efinal) は、最終予測誤差 efinal をベースにしたゼロラグの相関係数r0を出力します。

aの根がすべて単位円の内側にあるかどうかをチェックする簡単で高速な方法は、kの各要素の大きさが1未満かどうかをチェックすることです。

stable = all(abs(poly2rc(a))<1)

例題
つぎの多項式係数をもつIIRフィルタを考えます。

a = [1.0000   0.6149   0.9899   0.0000   0.0031  -0.0082];
efinal = 0.2;
その反射係数表現は、つぎのようになります。

[k,r0] = poly2rc(a,efinal)
k =
    0.3090
    0.9801
    0.0031
    0.0081
   -0.0082
r0 =
    5.6032

制限

任意のiに対して、abs(k(i)) == 1の場合は、反射係数を求めることは、条件数の悪い問題になります。この場合、poly2rcは、いくつかのNaNを出力し、ワーニングメッセージを表示します。

アルゴリズム

poly2rcは、つぎの再帰的関係を使います。

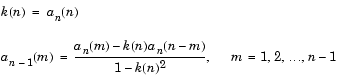
この関係は、Levinson再帰法(参考文献[1])に基づいています。これを実現するために、poly2rcは、aの最初の要素を空行列とし、その後で、aの要素を反転してループにより上の計算を行います。各ループの反復iについて、この関数は、つぎのことを行います。

1. k(i)をa(i)と設定します。
2. 上記の2番目の関係をベクトルaの1からiまでの要素に適用します。

   a = (a-k(i)*fliplr(a))/(1-k(i)^2);

参考

ac2rc	自己相関列を反射係数に変換
latc2tf	ラティスフィルタから伝達関数への変換
latcfilt	ラティスおよびラティス-ラダーフィルタの実現
poly2ac	予測多項式を自己相関列に変換
rc2poly	反射係数から多項式係数への変換
tf2latc	伝達関数からラティスフィルタへの変換

参考文献

[1] Kay, S.M. Modern Spectral Estimation, Englewood Cliffs, NJ, Prentice-Hall, 1988.

poly2lsf

polyscale