pade (Control System Toolbox関数リファレンス)

むだ時間をもつモデルのPade近似

表示

[num,den] = pade(T,N)
pade(T,N)

sysx = pade(sys,N)
sysx = pade(sys,NI,NO,Nio)

詳細

pade は、有理LTIモデルを使って、むだ時間の近似を行います。そのような近似は、連続系システムにおける伝達遅れやむだ時間などの時間遅延の影響をモデル化するのに役立ちます。秒のむだ時間のLaplace変換は、です。この指数伝達関数は、Pade近似公式[1]を使って有理伝達関数で近似されます(参考文献[1])。

[num,den] = pade(T,N) は、連続系遅延のN次(対角)Pade近似を伝達関数型で出力します。行ベクトルnumおよびden には、のべき乗の降順に並べた分子と分母の係数が含まれています。numとdenは、いずれも N次多項式です。

左辺の引数を設定しないと、

pade(T,N)

は、N次のPade近似のStep応答と位相応答をプロットし、むだ時間Tをもつモデルの正確な応答と比較します。Pade近似は、すべての周波数において単位ゲインをもっていることに注意してください。

sysx = pade(sys,N) は、連続時間むだ時間システムsysの遅延のない近似sysxを出力します。すべてのむだ時間は、それらのN次のPade近似で置き換えられます。遅れをもつLTIモデルの詳細については、マニュアルの"時間遅れ"を参照してください。

sysx = pade(sys,NI,NO,Nio)は、各入力、出力、I/Oの遅れに対して、個々に近似次数を設定します。これらの近似次数は、つぎのような整数NI、NO、Nioからなる配列で与えられます。

NI(j)は、j番目の入力チャンネルに対する近似次数

NO(i)は、i番目の出力チャンネルに対する近似次数

Nio(i,j)は、入力jから出力iまでのI/Oの遅れに対する近似次数

スカラ値を使って、一様な近似次数を設定することもでき、また、入力、出力、I/Oの遅れがない場合は、[]を設定することもできます。

例題

0.1秒のI/O遅れの3次Pade近似を計算し、真の遅延の時間応答と周波数応答をその近似と比較します。

pade(0.1,3)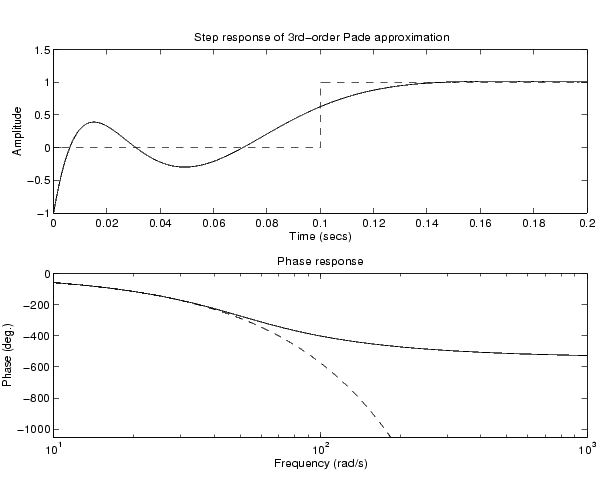

制限

高次のPade近似は、ある部分に集中した極の集合を伴う伝達関数を出力します。そのような極構成は、摂動の影響を非常に受け易いので、次数Nが10を超えるようなPade近似は避けてください。

参考
c2d 連続システムの離散化

delay2z 遅れをもつ離散のLTIモデルの伝達関数を有理関数に変換するか、または、周波数応答位相情報の中にFRDの遅れを含ませます。

参考文献

[1] Golub, G. H. and C. F. Van Loan, Matrix Computations, Johns Hopkins University Press, Baltimore, 1989, pp. 557-558.

ord2

parallel