| Control System Toolbox関数リファレンス | |
表示
rsys = modred(sys,elim) rsys = modred(sys,elim,'mdc') rsys = modred(sys,elim,'del')
詳細
modred
は、連続系または離散系状態空間モデルsysの低次元化を行ないます。この関数は、通常、balrealと共に使用します。2つの低次元化法を使用することができます。
rsys = modred(sys,elim)、 または、 rsys = modred(sys,elim,'mdc')は、DCゲインを変化させないで(または、step応答で同じ正定状態をもつ)低次元化モデルrsysを作成します。インデックスベクトルelimは、削除する状態を設定します。結果として得られるモデルrsysは、削除した状態数(length(elim))だけ少なくなります。この方法は、削除される状態の導関数をゼロに設定し、残りの状態に対する解を求めることから成り立っています。rsys = modred(sys,elim,'del')は、elimで設定した状態を削除するだけです。この方法は、DCゲインが不変化であることを保証しませんが、周波数領域での近似は、良くなる傾向があります(つぎの例を参照)。状態空間モデルsysがbalrealで平衡化され、グラミアンが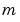
個の小さな対角要素をもつ場合、modredで最後から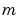
個の状態量を削除することにより、モデル次数を低減することができます。
例題
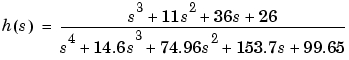
低次元化するために、まず、balrealを使って、平衡化された状態空間実現を計算します。
h = tf([1 11 36 26],[1 14.6 74.96 153.7 99.65]) [hb,g] = balreal(h) g'
ans = 1.3938e-01 9.5482e-03 6.2712e-04 7.3245e-06
平衡化されたグラミアンの最後から3つの対角要素は小さいので、DCゲインを変化させない方法と直接削除方法共に使って、modredで最後の3つの状態を削除します。
hmdc = modred(hb,2:4,'mdc') hdel = modred(hb,2:4,'del')
hmdcとhdelは、いずれも1次モデルです。それらのBode応答をオリジナルのモデル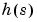
のBode応答と比較します。
bode(h,'-',hmdc,'x',hdel,'*')
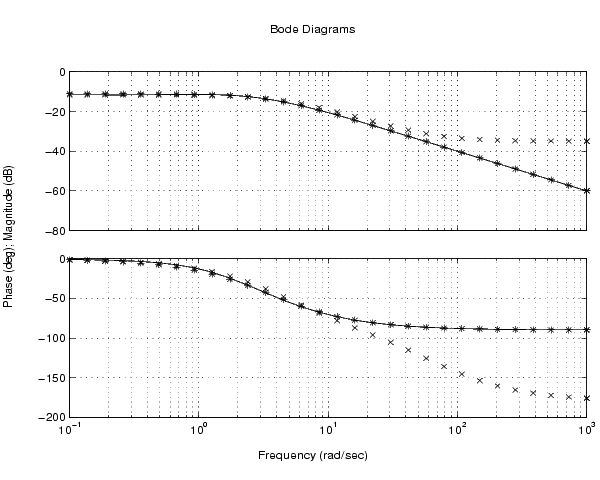
低次元化されたモデルhdelは、明らかに、より適切な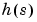
の周波数領域近似になっています。つぎに、Step応答を比較します。
step(h,'-',hmdc,'-.',hdel,'--')
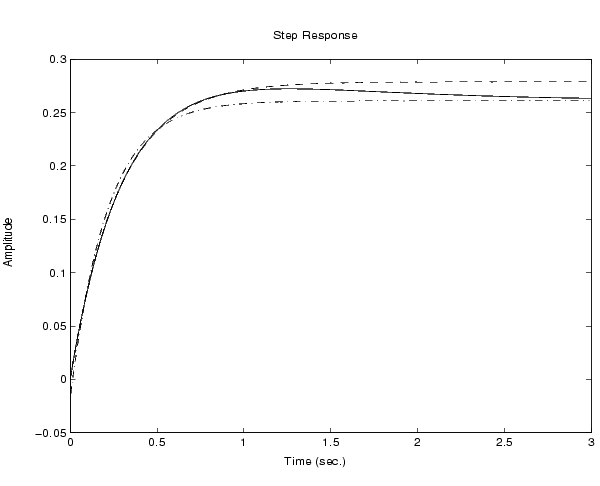
hdelは、過渡的挙動を正確に反映しますが、真の定常状態応答を反映するのはhmdcのみです。
アルゴリズム
DCゲインを変化させない方法のアルゴリズムは、つぎのとおりです。連続系モデル
に対して、状態ベクトルは残されるもの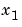
と削除されるもの
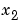に分けられます。
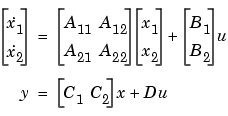
つぎに、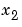
の導関数をゼロに設定し、結果として得られる方程式を
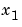について解きます。低次元化されたモデルは、以下によって与えられます。
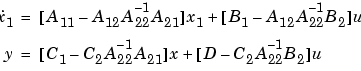
離散系の場合、つぎのように設定することにより同様に扱います。
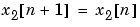
制限
DCゲインを変化させない方法の場合、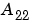
は連続系で正則でなければならず、
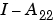は離散系で正則でなければなりません。
参考
balreal
minreal
| | minreal | ndims | |