fminsearch (MATLAB Function 参考文献)

多変数関数の最小化

表示

x = fminsearch(fun,x0)
x = fminsearch(fun,x0,options)
x = fminsearch(fun,x0,options,P1,P2,...)
[x,fval] = fminsearch(...)
[x,fval,exitflag] = fminsearch(...)
[x,fval,exitflag,output] = fminsearch(...)

詳細

fminsearch は、初期推定値から、多変数スカラ関数の最小値を検出します。これは、一般には、制約のない非線形最適化と云われます。

x = fminsearch(fun,x0) は、点 x0 を初期推定値とし、fun に記述される関数の極小値 x を求めます。x0 は、スカラ、ベクトル、行列のいずれでも可能です。

x = fminsearch(fun,x0,options) は、構造体 options で指定された最適化パラメータを使って最小化します。関数 optimset を使って、つぎのパラメータを定義します。fminsearch は、つぎの options 構造体フィールドを使います。

Display - 表示レベル。off は、出力を表示しません。iter は、各ステップで出力を表示します。final は、最終出力のみを表示します。

MaxFunEvals - 関数計算の可能な回数の最大回数

MaxIter - 可能な繰り返し回数の最大回数

TolFun - 関数値での終了のトレランス

TolX - xでの終了のトレランス

x = fminsearch(fun,x0,options,P1,P2,...) は、問題に依存したパラメータ P1、P2 等を、関数 fun に直接渡します。オプションを設定しない場合は、options = [] を使ってください。

[x,fval] = fminsearch(...) は、解 x で、目的関数 fun の値を、fval に出力します。

[x,fval,exitflag] = fminsearch(...) は、fminsearch の終了条件を記述する exitflag 値を出力します。

> 0 は、関数が、解 x に収束することを示します。

0 は、関数計算回数が、設定値に達したことを示します。

< 0 は、関数が解に収束しないことを示します。

[x,fval,exitflag,output] = fminsearch(...) は、最適化に関する情報を含む構造体 output を出力します。

output.algorithm - 使用するアルゴリズム

output.funcCount - 関数計算回数

output.iterations - 使用した繰り返し回数

引数

fun は、最小化される関数です。この関数は、スカラ x を受け入れ、x で計算される目的スカラ関数 f を出力します。関数 fun は、@を使って指定することもできます。

x = fminsearch(@myfun,x0,A,b)

ここで、myfun は、つぎのような MATLAB 関数です。

function f = myfun(x)
f = ...            % Compute function value at x

fun は、インライン関数としても定義できます。

x = fminsearch(inline('sin(x*x)'),x0,A,b);

他の引数は、表示記述で説明したものです。

例題

多次元最小化の古典的な例題は、Rosenbrock のバナナ関数です。

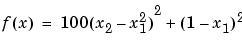
最小化は、(1,1) で生じ、値は 0 です。伝統的な出発点は、(-1.2,1) です。M-ファイル banana.m は、関数を定義します。

function f = banana(x)
f = 100*(x(2)-x(1)^2)^2+(1-x(1))^2;

ステートメント

[x,fval] = fminsearch(@banana,[-1.2, 1])

は、つぎの結果を出力します。

x =

    1.0000    1.0000

fval =

    8.1777e-010

この値は、最適化作業が、4桁の精度で値ゼロの近傍をもつものを探索したことを示します。

banana.m に2番目のパラメータを加えることにより、点 [a,a^2] に最小化の位置が移動します。

function f = banana(x,a)
nargin < 2,  a = 1; end
f = 100*(x(2)-x(1)^2)^2+(a-x(1))^2;

の場合、ステートメント

[x,fval] = fminsearch(@banana, [-1.2, 1], ...
   optimset('TolX',1e-8), sqrt(2));

は、新しいパラメータを sqrt(2) に設定し、x に関して、デフォルト以上の精度で、最小値を求めます。

アルゴリズム

fminsearch は、参考文献 [1] のシンプレックスサーチ法を使います。この方法は、数値的な勾配、または、解析的勾配を使わない直接サーチ法です。

n が、x の長さの場合、n 次元空間の中のシンプレックスは、n+1 個の頂点を示すベクトルにより特徴付けられます。2次元空間の場合、シンプレックスは三角形になり、3次元空間の場合四面体になります。サーチの各ステップで、カレントシンプレックスの中、または、近くの新しい点が生成されます。新しい点での関数値は、シンプレックスの頂点での関数値と比較され、その内の一つの頂点が新しい点、新しいシンプレックスを与える点で置き換えられます。このステップは、シンプレックスの直径が、指定したトレランスの値より小さくなるまで、繰り返されます。

制限

fminsearch は、解の近傍で不連続が生じなければ、不連続に関しても取り扱えます。fminsearch は、局所的な解のみを求める可能性があります。

fminsearch は、実数に対してのみ最小化を行います。それで、x は、実数のみから構成され、f(x) も実数のみを出力します。x が複素数変数の場合、実数部と虚数部に分ける必要があります。

参考

fminbnd, optimset, function_handle, inline

参考文献

Lagarias, J.C., J. A. Reeds, M. H. Wright, and P. E. Wright, "Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions," SIAM Journal of Optimization, Vol. 9 Number 1, pp. 112-147, 1998.

fmins fopen