fmins (MATLAB Function 参考文献)

多変数関数の最小化

注意この関数名は、リリース 11(MATLAB 5.3)の fminsearch に変更されました。fmins は、リリース11の間は、サポートされますが、将来は、削除される予定なので、fminsearch を使うことをお勧めします。

表示

x = fmins('fun',x0)
x = fmins('fun',x0,options)
x = fmins('fun',x0,options,[],P1,P2, ...)
[x,options] = fmins(...)

詳細

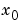x = fmins('fun',x0) は、の近傍で、fun(x) の極小値になるベクトル x を戻します。

x = fmins('fun',x0,options) は、上のものと同じですが、コントロールパラメータ options を使います。

x = fmins('fun',x0,options,[],P1,P2,...) は、上と同じですが、引数を目的関数 fun(x,P1,P2, ...) に渡します。デフォルト値を使う場合は、options に空行列を設定してください。

[x,options] = fmins(...) は、options(10) に使用したステップ回数を出力します。

引数

x0
スタートベクトル

P1,P2...
fun に渡す引数

[]
Optimization Toolbox の fminu と互換になるために必要な引数

fun
最小化される目的関数名を含む文字列。fun(x) は、ベクトル変数のスカラ値関数です。

options
コントロールパラメータベクトル。options の18要素の内、3つだけがfmins で参照されます。Optimization Toolbox の関数では、他のものも使用します。fmins で使用する 3つのコントロール options は、
options(1) -- 非ゼロの場合、解の算出作業状況が表示されます。options(1) のデフォルト値は0です。

options(2) and options(3) -- これは、それぞれ、x と function(x) に関する終了条件のトレランスです。デフォルト値は、 1.e-4です。

options(14) -- ステップの最大回数で、デフォルト値は、500 0です。

`x0`	スタートベクトル
`P1,P2...`	`fun` に渡す引数
`[]`	Optimization Toolbox の `fminu` と互換になるために必要な引数
`fun`	最小化される目的関数名を含む文字列。`fun(x)` は、ベクトル変数のスカラ値関数です。
`options`	コントロールパラメータベクトル。`options` の18要素の内、3つだけが`fmins` で参照されます。Optimization Toolbox の関数では、他のものも使用します。`fmins` で使用する 3つのコントロール `options` は、 `options(1)` -- 非ゼロの場合、解の算出作業状況が表示されます。`options(1)` のデフォルト値は0です。 `options(2)` and `options(3)` -- これは、それぞれ、`x` と `function(x)` に関する終了条件のトレランスです。デフォルト値は、 `1.e-4`です。 `options(14)` -- ステップの最大回数で、デフォルト値は、`500` 0です。

例題

多次元最小化の古典的な例題は、Rosenbrock のバナナ関数です。

最小値は、(1,1)で生じ、値は 0です。伝統的な出発点は、 (-1.2,1)です。M-ファイル banana.m は、関数を定義します。

function f = banana(x)
f = 100*(x(2)-x(1)^2)^2+(1-x(1))^2;

ステートメント

[x,out] = fmins('banana',[-1.2, 1]);
x
out(10)

を使って、つぎの結果を得ます。

x =

    1.0000    1.0000

ans =

    165

この値は、最適化作業により、165ステップで、少なくとも小数点以下4桁のものが求まっていることを示しています。

banana.m に2番目のパラメータを加えることにより、点 [a,a^2] に最小化の位置が移動します。

function f = banana(x,a)
if nargin < 2, a = 1; end
f = 100*(x(2)-x(1)^2)^2+(a-x(1))^2;

そして、ステートメント

[x,out] = fmins('banana', [-1.2, 1], [0, 1.e-8], [], sqrt(2));

は、新しいパラメータに sqrt(2) を設定し、デフォルト値よりも、より精度の高い最小値を求めます。

アルゴリズム

アルゴリズムは、参考文献に記述されている Nelder-Mead のシンプレックスサーチを使います。この方法は、勾配や他の微分情報を必要としない直接サーチ法です。n が、x の長さの場合、n 次元空間の中のシンプレックスは、n+1 個の頂点を示すベクトルにより特徴付けられます。2次元空間の場合、シンプレックスは三角形になり、3次元空間の場合四面体になります。

サーチの各ステップで、カレントシンプレックスの中、または、近くの新しい点が生成されます。新しい点での関数値は、シンプレックスの頂点での関数値と比較され、その内の一つの頂点が新しい点、新しいシンプレックスを与える点で置き換えられます。このステップは、シンプレックスの直径が、指定したトレランスの値より小さくなるまで、繰り返されます。

参考
fmin 1変数関数の最小化

Optimization Toolbox の中の foptions (または、help foptionsと入力)。

参考文献

[1] Nelder, J. A. and R. Mead, "A Simplex Method for Function Minimization," Computer Journal, Vol. 7, p. 308-313.

[2] Dennis, J. E. Jr. and D. J. Woods, "New Computing Environments: Microcomputers in Large-Scale Computing," edited by A. Wouk, SIAM, 1987, pp. 116-122.

fminbnd fminsearch