Mathematics

例題：電気力学問題

この例題は、偏微分方程式システムの解を示すものです。問題は、電気力学を使ったものです。これは、区間の両端に境界層があり、解は、短い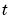で急激に変化するものです。

PDEs は、つぎのようになります。

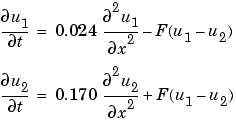
ここで、

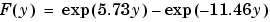です。この方程式は、時間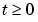に対して、区間 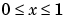で成り立ちます。

解 は、初期条件

と境界条件

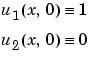
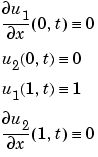
注意    デモ pdex4 は、この例題をすべてコード化されています。デモは、単一のM-ファイルの中に、必要なすべてのサブ関数を設定しています。デモを実行するには、コマンドラインで、pdex4と入力してください。詳細は、PDE Solver 基本的なシンタックス and PDE問題の表現を参照してください。

1 PDEの書き換え   pdepeで期待されている型で、方程式は、つぎのようになります。

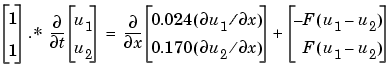
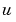の偏微分係数の境界条件は、流量の項で記述される必要があります。pdepeで期待される型で、左境界条件

と右境界条件

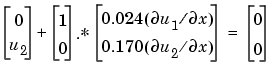
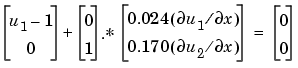
2 MATLAB の中でのPDEのコード化   上で示した型で、PDEを書き直した後、pdepeで使用可能なような関数として、コード化できます。関数は、つぎの型をしています。

[c,f,s] = pdefun(x,t,u,dudx)

ここで、c, f, s は、式 17-3の中で、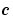, , 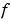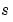に対応しています。

function [c,f,s] = pdex4pde(x,t,u,DuDx)
c = [1; 1]; 
f = [0.024; 0.17] .* DuDx; 
y = u(1) - u(2);
F = exp(5.73*y)-exp(-11.47*y);
s = [-F; F];  

3 初期条件関数をコード化   初期条件関数は、つぎの型をしている必要があります。

u = icfun(x)

下のコードは、MATLAB関数pdex4icの中の初期条件を表現しています。

function u0 = pdex4ic(x);
u0 = [1; 0]; 

4 境界条件関数をコード化   境界条件関数は、つぎの型をしている必要があります。

[pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)

下のコードは、MATLAB関数pdex4bcの中で境界条件の要素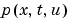 and 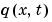(式 nbsp;17-5)を計算します。

function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
pl = [0; ul(2)]; 
ql = [1; 0];     
pr = [ur(1)-1; 0]; 
qr = [0; 1];     

5 解に対するメッシュ点を選択   解は、短い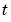で急激に変化します。プログラムは、この急激な変化に追従するように時間でのステップサイズを選択します。しかし、プロットの中でも、この挙動を見るには、出力時間をそれに応じて選択する必要があります。[0,1]の両端で、解に境界層があり、メッシュ点は、この急激な変化に追従するように配置する必要があります。解の挙動を表すメッシュを選択するために、いくつかの実験をする必要があります。

x = [0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
t = [0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];

6 PDE ソルバの適用   例題は、m = 0をもつpdepe、関数 pdex4pde, pdex4ic, pdex4bcをコールし、pdepeが解を計算する位置を、xとtでメッシュを使って定義します。pdepe関数は、3次元配列solの中に数値解を出力します。ここで、sol(i,j,k) は、t(i) とx(j)で計算した解の k番目の要素です。

m = 0;
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);

7 結果の視覚化   サーフェスプロットが、解要素の挙動を表示します。

u1 = sol(:,:,1);
u2 = sol(:,:,2);

figure
surf(x,t,u1)
title('u1(x,t)')
xlabel('Distance x')
ylabel('Time t')



figure
surf(x,t,u2)
title('u2(x,t)')
xlabel('Distance x')
ylabel('Time t')

PDE ソルバ性能の改良

参考文献