| Spline Toolbox | |
Put together a function in stform
Syntax
Description
stmak(centers,coefs)
returns the stform of the function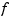 
given by
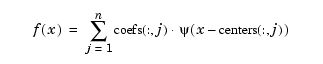
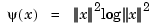
the thin-plate spline basis function, and with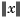 
denoting the Euclidean norm of the vector 
.
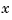centers and coefs must be matrices with the same number of columns.
st = stmak(centers,x,type) stores in st the stform of the function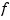 
given by
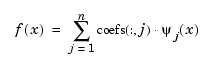
with the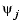 
as indicated by the string type, which can be one of the following:
'tp00', for the thin-plate spline;
'tp10', for the first derivative of a thin-plate spline wrto its first argument;
'tp01', for the first derivative of a thin-plate spline wrto its second argument;
'tp', the default.
st = stmak(centers,coefs,type,interv)
also specifies the basic interval for the stform, with interv{j} specifying, in the form [a,b], the range of the jth variable. The default for interv is the smallest such box that contains all the given centers.
Examples
Example 1. The following generates the figure below, of the thin-plate spline basis function,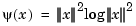 
, but suitably restricted to show that this function is negative near the origin. For this, the extra lines are there to indicate the zero level.
inx = [-1.5 1.5]; iny = [0 1.2];fnplt(stmak([0;0],1),{inx,iny})hold on, plot(inx,repmat(linspace(iny(1),iny(2),11),2,1),'r')view([25,20]),axis off, hold off
Example 2. We now also generate and plot, on the very same domain, the first partial derivative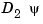 
of the thin-plate spline basis function, with respect to its second argument.
inx = [-1.5 1.5]; iny = [0 1.2];fnplt(stmak([0;0],[1 0],'tp01',{inx,iny}))view([13,10]),shading flat,axis off
Note that, this time, we have explicitly set the basic interval for the stform.
The resulting figure, below, shows a very strong variation near the origin. This reflects the fact that the second derivatives of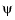 
have a logarithmic singularity there.
See Also
| | stcol | tpaps | |
, 
, 
, and 
the partial derivative of 
wrto 
, 
, and 
the partial derivative of 
wrto 
, 
