sectf (Robust Control Toolbox)

Robust Control Toolbox

sectf

State-space sector bilinear transformation.

Syntax

[ag,bg1,,dg22,at,bt1,,dt21,dt22] = sectf(af,bf1,,df22,secf,secg) 
[ag,bg,cg,dg,at,bt1,,dt21,dt22] = sectf(af,bf,cf,df,secf,secg) 
[tssg,tsst] = sectf(tssf,secf,secg) 
[ssg,tsst] = sectf(ssf,secf,secg)

Description
sectf may be used to transform conic-sector control system performance specifications into equivalent H-norm performance specifications. Given a two-port state-space system F(s) := tssf, sectf computes a linear-fractionally-transformed two-port state-space system G(s) := tssg such that the channel-one Input-Output (I/O) pairs (u_g1, y_g1) of G(s) are in sector secg if and only if the corresponding I/O pairs of F(s) are in secf. Also computed is a two-port system T(s) such that G(s) is obtained via the MATLAB command tssg=lftf(tsst,tssf).

Input variables are:

The open loop plant F(s)

tssf
mksys(af,bf1,bf2,cf1,cf2,df11,df12,df21,df22,'tss'),

or

ssf
mksys(af,bf,cf,df)

Conic sector specifications for F(s) and G(s), respectively, in one of the following forms:

secg, secf
secg, secf
Sector inequality:

[-1,1] or [-1;1]

[0,Inf] or [0;Inf]

[A,B] or [A;B]

[a,b] or [a;b]

S

tsss

The open loop plant F(s)
`tssf`	`mksys(af,bf1,bf2,cf1,cf2,df11,df12,df21,df22,'tss'),`
or
`ssf`	`mksys(af,bf,cf,df)`
Conic sector specifications for F(s) and G(s), respectively, in one of the following forms:
`secg, secf`	`secg, secf`	Sector inequality:
	`[-1,1]` or `[-1;1]`
	`[0,Inf]` or `[0;Inf]`
	`[A,B]` or `[A;B]`
	`[a,b]` or `[a;b]`
	`S`
	`tsss`

where A,B are scalars in [-, ] or square matrices; a,b are vectors; S=[S11 S12;S21,S22] is a square matrix whose blocks S11,S12,S21,S22 are either scalars or square matrices; tsss is a two-port system tsss=mksys(a,b1,b2,,'tss') with transfer function

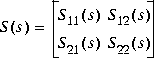
Output variables are:The transformed plant G(s): tssg mksys(ag,bg1,bg2,cg1,cg2,dg11,dg12,dg21,dg22,'tss'), or ssg mksys(ag,bg,cg,dg) The linear fractional transformation T(s): tsst mksys(at,bt1,bt2,ct1,ct2,dt11,dt12,dt21,dt22,'tss')

	*The transformed plant G(s):*
`tssg`	`mksys(ag,bg1,bg2,cg1,cg2,dg11,dg12,dg21,dg22,`'`tss`'`),`
	or
`ssg`	`mksys(ag,bg,cg,dg)` The linear fractional transformation T(s):
`tsst`	`mksys(at,bt1,bt2,ct1,ct2,dt11,dt12,dt21,dt22,`'`tss`'`)`

Here tssf, tsst, and tssg are two-port state-space representations of F(s), T(s), and G(s).

If the input F(s) is specified as a standard state-space system ssf, then the sector transformation is performed on all channels of F(s), so that the output G(s) will likewise be returned in standard state-space form ssg.

Examples
The statement G(j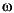) inside sector[-1, 1] is equivalent to the H inequality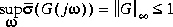

Given a two-port open-loop plant P(s) := tssp1, the command
tssp1 = sectf(tssp,[0,Inf],[-1,1]) computes a transformed P(s) := tssp1 such that an H feedback K(s), which places the closed-loop transformed system inside sector[-1, 1], also places the original system inside sector[0, ]. See Figure 1-14.

Figure 1-14: Sector Transform Block Diagram.

Here is a simple example of the sector transform.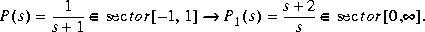

You can compute this by simply executing the following commands:

[A,B,C,D] = tf2ss(1,[1 1]); 
[a,b,c,d] = sectf(A,B,C,D,[-1,1],[0,Inf]);

The Nyquist plots for this transformation are depicted in Figure 1-15. The condition P₁(s) inside [0,

] implies that P₁(s) is stable and P₁(j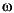

) is positive real, i.e.,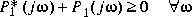

sectf is a M-file in the Robust Control Toolbox that uses the generalization of the sector concept of [3] described by [1]. First the sector input data Sf= secf and Sg=secg is converted to two-port state-space form; non-dynamical sectors are handled with empty a, b1, b2, c1, c2 matrices. Next the equation

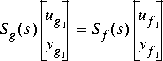
is solved for the two-port transfer function T(s) from 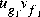to

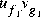. Finally, the function lftf is used to compute G(s) via one of the following:

tssg=lftf(tsst,tssg) 
ssg=lftf(tsst,ssg).

Figure 1-15: Example of Sector Transform.

Limitations
A well-posed conic sector must have 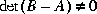or .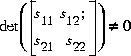

Also, you must have 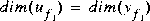since sectors are only defined for square systems.

See Also
lftf, hinf, system

References
[1] M. G. Safonov, Stability and Robustness of Multivariable Feedback Systems. Cambridge, MA: MIT Press, 1980.

[2] M. G. Safonov, E. A. Jonckheere, M. Verma and D. J. N. Limebeer, "Synthesis of Positive Real Multivariable Feedback Systems," Int. J. Control, vol. 45, no. 3, pp. 817-842, 1987.

[3] G. Zames, "On the Input-Output Stability of Time-Varying Nonlinear Feedback Systems -- Part I: Conditions Using Concepts of Loop Gain, Conicity, and Positivity," IEEE Trans. on Automat. Contr., AC-11, pp. 228-238, 1966.

riccond sfl, sfr