| Robust Control Toolbox | |
Generalized discrete algebraic Riccati solver.
Syntax
[p1,p2,lamp,perr,wellposed,p] = daresolv(a,b,q,r) [p1,p2,lamp,perr,wellposed,p] = daresolv(a,b,q,r,Type)
Description
Daresolv solves the discrete algebraic Riccati equation
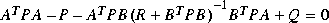
where P = P2/P1 is the solution for which the eigenvalues of A - RP are inside the unit disk. This solution exists and is unique provided that the associated discrete Hamiltonian matrix
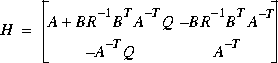
has no eigenvalues on the unit circle; otherwise, the flag wellposed is set to the string value 'FALSE'.
The input variables and output variables are otherwise identical to the continuous time case--see aresolv. If Type = 1 the eigenvector approach is used. If Type = 2 the Schur vector approach is used. The eigenvector approach is selected by default when no Type is specified, unless the Hamiltonian matrix is defective in which case the algorithm defaults to the Schur approach. The residual and closed loop eigenvalues are returned in variables perr and lamp.
Algorithm
The algorithm is essentially the same as that employed for the continuous version of this function, save for the difference in the discrete Hamiltonian. The matrices P1 and P2 are computed such that the columns of
form a basis for the stable eigenspace of the discrete Hamiltonian, i.e., the space spanned by the eigenvectors corresponding to eigenvalues in the unit disk. See aresolv.
Limitations
The Riccati equation is ill-posed if the Hamiltonian H has eigenvalues on the unit circle. In cases in which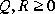 
, it suffices for the system (A,R,Q) to be both stabilizable and detectable to avoid eigenvalues on the unit circle; in this case, the unique stabilizing Riccati solution will be positive semidefinite.
See Also
are, cschur, aresolv, lqrc, reig, driccond
| cgloci, dcgloci | des2ss | |