bilin (Robust Control Toolbox)

Robust Control Toolbox

bilin

Multivariable bilinear transform of frequency (s or z).

Syntax

[ab,bb,cb,db] = bilin(a,b,c,d,ver,Type,aug)
[ssb] = bilin(ss,ver,Type,aug)

Description
Bilin computes the effect on a system of the frequency-variable substitution,

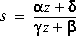
The variable Ver denotes the transformation direction:

Ver= 1, forward transform .

Ver=-1, inverse transform .

This transformation maps lines and circles to circles and lines in the complex plane. People often use this transformation to do sampled-data control system design [1] or, in general, to do shifting of j modes [2], [3], [4].

Bilin computes several state-space bilinear transformations such as Tustin, prewarped Tustin, etc., based on the Type you select:

1: Type = 'Tustin', Tustin transform: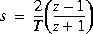

aug = T, the sampling period.

2: Type = 'P_Tust', prewarped Tustin: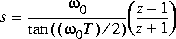

aug = [T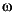

₀],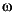

₀ is the prewarped frequency.

3: Type = 'BwdRec', backward rectangular: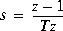

aug = T, the sampling period.

4: Type = 'FwdRec', forward rectangular: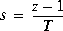

aug = T, the sampling period.

5: Type = 'S_Tust', shifted Tustin: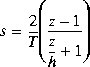

aug = [T h], is the "shift" coefficient.

6: Type = 'S_ftjw', shifted j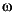-axis bilinear: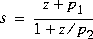

aug = [p₂p₁].

7: Type = 'G_Bilin', general bilinear: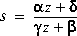

aug =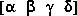

Examples
Consider the following continuous-time plant (sampled at 20 Hz)

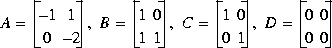Following is an example of four common "continuous to discrete" bilin transformations for the sampled plant:

ss = mksys(a,b,c,d); %use system data structure 
[sst] = bilin(ss,1,'Tustin',0.05); 
[ssp] = bilin(ss,1,'P_Tust',[0.05 40]);
[ssb] = bilin(ss,1,'BwdRec',0.05); 
[ssf] = bilin(ss,1,'FwdRec',0.05); 
w = logspace(-2,3,100) %frequency
svt = dsigma(sst,0.05,w); 
svp = dsigma(ssp,0.05,w); 
svb = dsigma(ssb,0.05,w); 
svf = dsigma(ssf,0.05,w);

.

Figure 1-3: Comparison of 4 Bilinear Transforms.

you can generate the continuous and discrete singular value Bode plots as shown in the Figure 1-3.

Note that the Nyquist frequency is at 20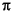 rad/sec.

Algorithm
bilin employs the state-space formulae in [3]:

See Also
lftf, sectf

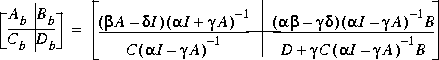
[1] G. F. Franklin and J. D. Powell, Digital Control of Dynamics System, Addison-Wesley, 1980.

[2]M. G. Safonov, R. Y. Chiang and H. Flashner, "H Control Synthesis for a Large Space Structure," AIAA J. Guidance, Control and Dynamics, 14, 3, pp. 513-520, May/June 1991.

[3] M. G. Safonov, "Imaginary-Axis Zeros in Multivariable HOptimal Control", in R. F. Curtain (editor), Modelling, Robustness and Sensitivity Reduction in Control Systems, pp. 71-81, Springer-Verlag, Berlin, 1987. Proc. NATO Advanced Research Workshop on Modeling, Robustness and Sensitivity Reduction in Control Systems, Groningen, The Netherlands, Dec. 1-5, 1986.

[4] R. Y. Chiang and M. G. Safonov, "H Synthesis using a Bilinear Pole Shifting Transform," AIAA, J. Guidance, Control and Dynamics, vol. 15, no. 5, pp. 1111-1117, September-October 1992.

balmr, schmr blkrsch, cschur