

| Robust Control Toolbox |   |
Block ordered real Schur form.
Ordered complex Schur form via complex Givens rotation.
Syntax
Description
Cschur computes a unitary similarity transformation V and a complex upper triangular matrix T for a real or complex matrix A such that
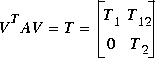
where T has the eigenvalues 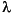 i(A) ordered on the diagonal according to the value of the variable
i(A) ordered on the diagonal according to the value of the variable Type:
Type = 1 -- 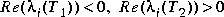 .
.
Type = 2 -- 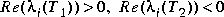 .
.
Type = 3 -- eigenvalue real parts in descending order.
Type = 4 -- eigenvalue real parts in ascending order.
Type = 5 -- modulus of eigenvalues in descending order.
Type = 6 -- modulus of eigenvalues in ascending order.
swap records the number of Givens rotations swaps it takes and variable m returns the number of "stable" eigenvalues of A (see rsf2csf or cgivens).
Blkrsch computes a block ordered real Schur form such that the resulting T matrix has four blocks
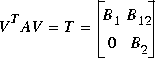
The input variable cut is the dimension of the square block B1. If Type is 1, cut is automatically set to m -- the number of eigenvalues of A with negative real parts.
Type = 1 -- 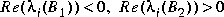 .
.
Type = 2 -- 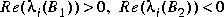 .
.
Type = 3 --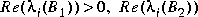
.
Type = 4 --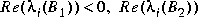 .
.
Type = 5 -- .
.
Type = 6 --.
Algorithm
blkrsch and cschur, are M-files in the Robust Control Toolbox. cschur uses schur, rsf2csf and the complex Givens rotation [1] to iteratively swap two adjacent diagonal terms according the style you select. blkrsch projects the resulting complex subspace onto the real.
Limitations
For blkrsch, the matrix A must have zero imaginary part.
See Also
cgivens, rsf2csf, schur
References
[1] Golub G. H. and C. F. Van Loan, Matrix Computations. Baltimore: Johns Hopkins University Press, 1983.
 | bilin | branch |  |