| Robust Control Toolbox | |
Balanced model reduction via truncated and Schur methods.
Syntax
[am,bm,cm,dm,totbnd,svh] = balmr(a,b,c,d,Type) [am,bm,cm,dm,totbnd,svh] = balmr(a,b,c,d,Type,aug) [am,bm,cm,dm,totbnd,svh] = schmr(a,b,c,d,Type) [am,bm,cm,dm,totbnd,svh] = schmr(a,b,c,d,Type,aug) [ssm,totbnd,svh] = balmr(ss,Type,aug) [ssm,totbnd,svh] = schmr(ss,Type,aug)
Description
Both balmr and schmr compute a kth order reduced model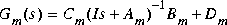
of a possibly non-minimal and not necessarily stable, nth order system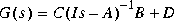
The n-vector svh contains the Hankel singular values of the stable and antistable projections of G(j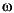
), i.e., the square-roots of eigenvalues of their reachability and observability grammians.
Three options are provided for both functions:
Type = 1, aug = k, size of reduced order model.
Type = 2, aug = tol, find a kth order reduced model such that the total error totbnd
is less than tol.
Type = 3, display svh and prompt for k. In this case, there is no need to assign
a value for aug.
balmr and schmr produce state-space realizations of the same transfer function Gm. The realization (Am, Bm, Cm, Dm) produced by balmr is balanced (see balreal or obalreal), whereas that produced by schmr algorithm is not. The schmr algorithm is numerically more robust than balmr and is thus to be preferred when the reduced model need not be balanced.
Algorithm
Balmr and schmr employ the algorithms described in [3] for implementing the balanced truncation model reduction procedure of [2], but unlike the original Moore algorithm, these algorithms bypass the numerically delicate preliminary step of computing a balanced minimal realization of G(s).
Unstable systems are handled via the M-function stabproj which splits G(s) into the sum of stable and antistable parts.
See Also
balreal, mrdemo, obalreal, ohklmr, bstschmr, bstschml
[1] A. J. Laub, M. T. Heath, C. C. Page, and R. C. Ward, "Computation of balancing transformations and other applications of simultaneous diagonalization algorithms," IEEE Trans. on Automat. Contr., AC-32, pp. 115-122, 1987.
[2] B. C. Moore, "Principal component analysis in linear systems: controllability, observability, and model reduction," IEEE Trans. on Automat. Contr., AC-26, pp. 17-31, 1981.
[3] M. G. Safonov and R. Y. Chiang, "A Schur Method for Balanced Model Reduction," IEEE Trans. on Automat. Contr., vol. AC-34, no. 7, pp. 729-733, July 1989.
| augss, augtf | bilin | |