SimMechanics    

Adding Sensors and Starting the Simulation

To measure the motion of the pendulum as it swings, you need to hook one or more Simulink Scope blocks to your model. The special library of Actuators and Sensor blocks gives you the means to input and output Simulink signals to and from SimMechanics models. Sensors allow you to watch the mechanical motion once you start the simulation, as the following explain:

Connecting and Configuring Pendulum Sensors

In this example, you measure the angular motion of the revolute joint:

  1. In the block library, open the Sensors and Actuators library. Drag and drop two Joint Sensor blocks into your model window.
  2. Open the Revolute block. Change Number of sensor/actuator ports from 0 to 2 using the spinner menu. Two open connector ports appear on either side of Revolute. Close Revolute.
  3. Connect these connector ports to the connector ports on the Joint Sensor blocks. The open connector ports change to solid .
  4. Open the Simulink Library Browser. From the Sinks library, drag and drop a Scope block and an XY Graph block into your model window. From the Signal Routing library, drag and drop a Mux block as well. Connect the Simulink outports > on the Joint Sensor blocks to the Scope and XY Graph blocks as shown.

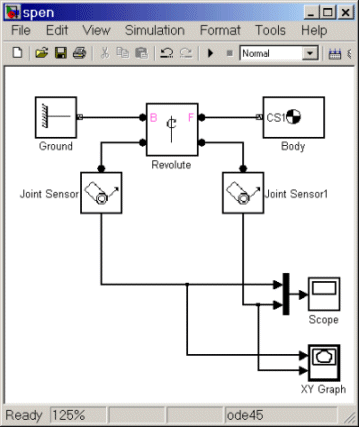
  1. The lines from the outports > to the Scope and XY Graph blocks are normal Simulink signal lines and can be branched. You cannot branch the lines connecting SimMechanics blocks to each another at the round connector ports .

  1. Open Joint Sensor. Select only the Angle check box. Open Joint Sensor1. Select only the Angular velocity check box. Leave the other defaults. Close both Sensor blocks.
  2. Save your model for future reference as spen.mdl.

You now need to configure the global parameters of your model before you can run it.

Configuring Simulation Parameters and Mechanical Environment Settings

The Simulation Parameters dialog box is a standard feature of Simulink. Reset its entries for this model to obtain more accurate simulation results.

  1. In the Simulink menu bar, open the Simulation menu and click Simulation parameters to open the Simulation Parameters dialog.
  2. Change Relative tolerance to 1e-6 and Absolute tolerance to 1e-4.
  1. If you want the simulation to stop after a finite time, change Stop time to a finite number of seconds. The pendulum period is approximately 1.6 sec.

  1. Close the Simulation Parameters dialog box.

A special feature of SimMechanics models is the Mechanical Environment Settings dialog box.

  1. In the Simulink menu bar, open the Simulation menu and click Mechanical environment to open the Mechanical Environment Settings dialog.
  1. Note the default Gravity vector and units: [0 -9.81 0] m/s2, which points in the -y direction, as shown in Figure 2-2. Gravitational acceleration g = 9.81 m/s2.

  1. Close the Mechanical Environment Settings dialog.

Starting and Interpreting the Motion

You can now start your simulation and watch the pendulum motion via the Scope and XY Graph blocks:

  1. Open the XY Graph block dialog box. Set the following parameters.

    Parameter
    		 Value
    x-min
    		 0
    x-max
    		 200
    y-min
    		 -500
    y-max
    		 500
  1. Leave Sample time at default and close the dialog.

  1. Open the Scope block and start the model. The XY Graph opens automatically when you start the simulation.
  2. View the full motion of both angle and angular velocity (in degrees and degrees per second, respectively) as functions of time in Scope. Click Autoscale if the motion is not fully visible.

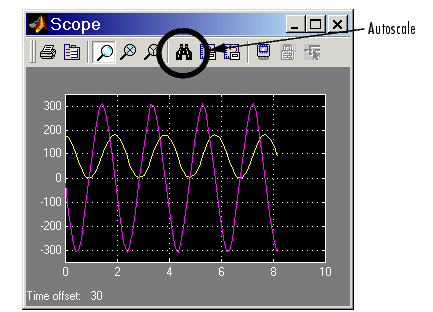
Angle and Angular Velocity of the Simple Pendulum as Functions of Time

  1. The motion is periodic but not simple harmonic (sinusoidal), because the amplitude of the swing is so large (180 degrees from one turning point to the other). Note that the zero of angle is the initial horizontal angle, not the vertical. The zeros of motion are always the initial conditions.

The XY Graph shows the angle versus angular velocity, with no explicit time axis. These two variables trace out a figure similar to an ellipse, because of the conservation of total energy E:

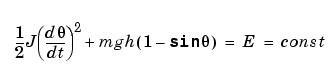
where J = Izz + mL2/4 is the inertial moment of the rod about its pivot point (not the center of gravity). The two terms on the left side of this equation are the kinetic and potential energies, respectively. The coordinate-velocity space is the phase space of the system.

Phase Space Plot of Simple Pendulum Motion: Angular Velocity Versus Angle

The directionality of the Revolute Joint assumes that the rotation axis lies in the +z direction. Looking at the pendulum from the front, follow Figure 2-1, Figure 2-2, and Figure 2-3. Positive angular motion from this perspective is counterclockwise, following the right-hand rule.

The next tutorial walks you through visualizing and animating this same simple pendulum model.


  Configuring a Joint Block Visualizing a Simple Pendulum