

| Partial Differential Equation Toolbox |   |
Examples of Eigenvalue Problems
This section describes the solution of some eigenvalue PDE problems. The problems are solved using the graphical user interface (GUI) and the command-line functions of the PDE Toolbox. The problems include
Eigenvalues and Eigenfunctions for the L-Shaped Membrane
The problem of finding the eigenvalues and the corresponding eigenfunctions of an L-shaped membrane is of interest to all MATLAB users, since the plot of the first eigenfunction is the logo of The MathWorks. In fact, you can compare the PDE Toolbox computed eigenvalues and eigenfunctions to the ones produced by the MATLAB function membrane.
The problem is to compute all eigenmodes with eigenvalues < 100 for the eigenmode PDE problem
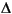 u =
u = 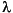 u
u
on the geometry of the L-shaped membrane. u = 0 on the boundary (Dirichlet condition).
Using the Graphical User Interface
With the pdetool GUI active, check that the current mode is Generic Scalar. Then draw the L-shape as a polygon with corners in (0,0), (-1,0), (-1,-1), (1,-1), (1,1), and (0,1).
There is no need to define any boundary conditions for this problem since the default condition -- u = 0 on the boundary -- is the correct one. Therefore, you can continue to the next step: to initialize the mesh. Refine the initial mesh twice. Defining the eigenvalue PDE problem is also easy. Open the PDE Specification dialog box and select Eigenmodes. The default values for the PDE coefficients, c = 1, a = 0, d = 1, all match the problem description, so you can exit the PDE Specification dialog box by clicking the OK button.
Open the Solve Parameters dialog box by selecting Parameters . . . from the Solve menu. The dialog box contains an edit box for entering the eigenvalue search range. The default entry is [0 100], which is just what you want.
Finally, solve the L-shaped membrane problem by clicking the = button. The solution displayed is the first eigenfunction. The value of the first (smallest) eigenvalue is also displayed. You find the number of eigenvalues on the information line at the bottom of the GUI. You can open the Plot Selection dialog box and choose which eigenfunction to plot by selecting from a pop-up menu of the corresponding eigenvalues.
Using Command-Line Functions
The geometry of the L-shaped membrane is described in the file lshapeg.m and the boundary conditions in the file lshapeb.m.
First, initialize the mesh and refine it twice using the command line functions at the MATLAB prompt:
[p,e,t]=initmesh('lshapeg'); [p,e,t]=refinemesh('lshapeg',p,e,t); [p,e,t]=refinemesh('lshapeg',p,e,t);
Recall the general eigenvalue PDE problem description:
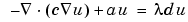
This means that in this case you have c = 1, a = 0, and d = 1. The syntax of pdeeig, the eigenvalue solver in the PDE Toolbox, is
The input argument r is a two-element vector indicating the interval on the real axis where pdeeig searches for eigenvalues. Here you are looking for eigenvalues < 100, so the interval you use is [0 100].
Now you can call pdeeig and see how many eigenvalues you find:
There are 19 eigenvalues smaller than 100. Plot the first eigenmode and compare it to the MATLAB membrane function:
membrane can produce the first 12 eigenfunctions for the L-shaped membrane. Compare also the 12th eigenmodes:
Looking at the following eigenmodes, you can see how the number of oscillations increases. The eigenfunctions are symmetric or antisymmetric around the diagonal from (0,0) to (1,-1), which divides the L-shaped membrane into two mirror images. In a practical computation, you could take advantage of such symmetries in the PDE problem, and solve over a region half the size. The eigenvalues of the full L-shaped membrane are the union of those of the half with Dirichlet boundary condition along the diagonal (eigenvalues 2, 4, 7, 11, 13, 16, and 17) and those with Neumann boundary condition (eigenvalues 1, 3, 5, 6, 10, 12, 14, and 15).
The eigenvalues 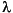 8 and
8 and 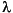 9 make up a double eigenvalue for the PDE at around 49.64. Also, the eigenvalues
9 make up a double eigenvalue for the PDE at around 49.64. Also, the eigenvalues 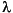 18 and
18 and 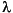 19 make up another double eigenvalue at around 99.87. You may have gotten two different but close values. The default triangulation made by
19 make up another double eigenvalue at around 99.87. You may have gotten two different but close values. The default triangulation made by initmesh is not symmetric around the diagonal, but a symmetric grid gives a matrix with a true double eigenvalue. Each of the eigenfunctions u8 and u9 consists of three copies of eigenfunctions over the unit square, corresponding to its double second eigenvalue. You may not have obtained the zero values along a diagonal of the square -- any line through the center of the square may have been computed. This shows a general fact about multiple eigenvalues for symmetric matrices; namely that any vector in the invariant subspace is equally valid as an eigenvector. The two eigenfunctions u8 and u9 are orthogonal to each other if the dividing lines make right angles. Check your solutions for that.
Actually, the eigenvalues of the square can be computed exactly. They are
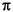 2
2
e.g., the double eigenvalue 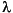 18 and
18 and 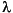 19 is 10
19 is 10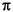 2, which is pretty close to 100.
2, which is pretty close to 100.
If you compute the FEM approximation with only one refinement, you would only find 16 eigenvalues, and you obtain the wrong solution to the original problem. You can of course check for this situation by computing the eigenvalues over a slightly larger range than the original problem.
You get some information from the printout in the MATLAB command window that is printed during the computation. For this problem, the algorithm computed a new set of eigenvalue approximations and tested for convergence every third step. In the output, you get the step number, the time in seconds since the start of the eigenvalue computation, and the number of converged eigenvalues with eigenvalues both inside and outside the interval counted.
Basis= 10, Time= 2.70, New conv eig= 0 Basis= 13, Time= 3.50, New conv eig= 0 Basis= 16, Time= 4.36, New conv eig= 0 Basis= 19, Time= 5.34, New conv eig= 1 Basis= 22, Time= 6.46, New conv eig= 2 Basis= 25, Time= 7.61, New conv eig= 3 Basis= 28, Time= 8.86, New conv eig= 3 Basis= 31, Time= 10.23, New conv eig= 5 Basis= 34, Time= 11.69, New conv eig= 5 Basis= 37, Time= 13.28, New conv eig= 7 Basis= 40, Time= 14.97, New conv eig= 8 Basis= 43, Time= 16.77, New conv eig= 9 Basis= 46, Time= 18.70, New conv eig= 11 Basis= 49, Time= 20.73, New conv eig= 11 Basis= 52, Time= 22.90, New conv eig= 13 Basis= 55, Time= 25.13, New conv eig= 14 Basis= 58, Time= 27.58, New conv eig= 14 Basis= 61, Time= 30.13, New conv eig= 15 Basis= 64, Time= 32.83, New conv eig= 16 Basis= 67, Time= 35.64, New conv eig= 18 Basis= 70, Time= 38.62, New conv eig= 22 End of sweep: Basis= 70, Time= 38.62, New conv eig= 22 Basis= 32, Time= 43.29, New conv eig= 0 Basis= 35, Time= 44.70, New conv eig= 0 Basis= 38, Time= 46.22, New conv eig= 0 Basis= 41, Time= 47.81, New conv eig= 0 Basis= 44, Time= 49.52, New conv eig= 0 Basis= 47, Time= 51.35, New conv eig= 0 Basis= 50, Time= 53.27, New conv eig= 0 Basis= 53, Time= 55.30, New conv eig= 0 End of sweep: Basis= 53, Time= 55.30, New conv eig= 0
You can see that two Arnoldi runs were made. In the first, 22 eigenvalues converged after a basis of size 70 was computed; in the second, where the vectors were orthogonalized against all the 22 converged vectors, the smallest eigenvalue stabilized at a value outside of the interval [0, 100], so the algorithm signaled convergence. Of the 22 converged eigenvalues, 19 were inside the search interval.
 | Example of a Hyperbolic Problem | L-Shaped Membrane with Rounded Corner |  |