

| Partial Differential Equation Toolbox |   |
Eigenvalues and Eigenmodes of a Square
Let us study the eigenvalues and eigenmodes of a square with an interesting set of boundary conditions. The square has corners in (-1,-1), (-1,1), (1,1), and (1,-1). The boundary conditions are as follows:
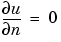
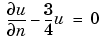
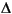 u =
u = 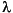 u
u
We are interested in the eigenvalues smaller than 10 and the corresponding eigenmodes, so the search range is [-Inf 10]. The sign in the generalized Neumann condition is such that there are negative eigenvalues.
Using the Graphical User Interface
Using the pdetool GUI in the Generic Scalar mode, draw the square using the Rectangle/square option from the Draw menu or the button with the rectangle icon. Then define the boundary conditions by clicking the  button and then double-click the boundaries to define the boundary conditions. On the right side boundary, you have the generalized Neumann conditions, and you enter them as constants: g = 0 and q = -3/4.
button and then double-click the boundaries to define the boundary conditions. On the right side boundary, you have the generalized Neumann conditions, and you enter them as constants: g = 0 and q = -3/4.
Initialize the mesh and refine it once by clicking the  and refine buttons or by selecting the corresponding options from the Mesh menu.
and refine buttons or by selecting the corresponding options from the Mesh menu.
Also, define the eigenvalue PDE problem by opening the PDE Specification dialog box and selecting the Eigenmodes option. The general eigenvalue PDE is described by
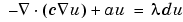
so for this problem you use the default values c = 1, a = 0, and d = 1. Also, in the Solve Parameters dialog box, enter the eigenvalue range as the MATLAB vector [-Inf 10].
Finally, click the = button to compute the solution. By default, the first eigenfunction is plotted. You can plot the other eigenfunctions by selecting the corresponding eigenvalue from a pop-up menu in the Plot Selection dialog box. The pop-up menu contains all the eigenvalues found in the specified range. You can also export the eigenfunctions and eigenvalues to the MATLAB main workspace by using the Export Solution . . . option from the Solve menu.
Using Command-Line Functions
The geometry description file and boundary condition file for this problem are called squareg.m and squareb2.m, respectively. Use the following sequence of commands to find the eigenvalues in the specified range and the corresponding eigenfunctions:
The eigenvalue PDE coefficients c, a, and d for this problem are c = 1, a = 0, and d = 1. You can enter the eigenvalue range r as the MATLAB vector [-Inf 10]. pdeeig returns two output arguments, the eigenvalues as an array l and a matrix v of corresponding eigenfunctions:
To plot the fourth eigenfunction as a surface plot, type
This problem is separable, i.e.,
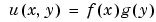
The functions f and g are eigenfunctions in the x and y directions, respectively. In the x direction, the first eigenmode is a slowly increasing exponential function. The higher modes include sinusoids. In the y direction, the first eigenmode is a straight line (constant), the second is half a cosine, the third is a full cosine, the fourth is one and a half full cosines, etc. These eigenmodes in the y direction are associated with the eigenvalues:
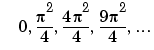
There are five eigenvalues smaller than 10 for this problem, and the first one is even negative (-0.4145). It is possible to trace the eigenvalues above in the eigenvalues of the solution. Looking at a plot of the first eigenmode, you can see that it is made up of the first eigenmodes in the x and y directions. The second eigenmode is made up of the first eigenmode in the x direction and the second eigenmode in the y direction.
Look at the difference between the first and the second eigenvalue:
Likewise, the fifth eigenmode is made up of the first eigenmode in the x direction and the third eigenmode in the y direction. As expected, l(5)-l(1) is approximately equal to 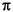 2. You can explore higher modes by increasing the search range to include eigenvalues greater than 10.
2. You can explore higher modes by increasing the search range to include eigenvalues greater than 10.
 | L-Shaped Membrane with Rounded Corner | Application Modes |  |