Model Browser User's Guide

Prediction Error Variance for Two-Stage Models

It is very useful to evaluate a measure of the precision of the model's predictions. You can do this by looking at Prediction Error Variance (PEV). Prediction error variance will tend to grow rapidly in areas outside the original design space. The following section describes how PEV is calculated for two-stage models.

For linear global models applying the variance operator to Equation 6-15 yields

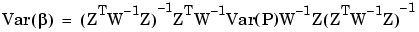• so

,

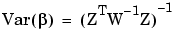(6-17)

since Var(P) = W. Assume that it is required to calculate both the response features and their associated prediction error variance for the i^th test. the predicted response features are given by

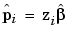
(6-18)

where 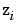is an appropriate global covariate matrix. Applying the variance operator to Equation 6-18 yields

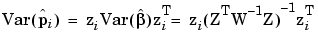
(6-19)

In general, the response features are non-linear functions of the local fit coefficients. Let 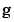denote the non-linear function mapping 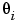onto 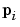. Similarly let 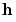denote the inverse mapping.

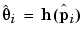
(6-20)

Approximating 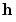using a first order Taylor series expanded about 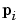(the true and unknown fixed population value) and after applying the variance operator to the result,

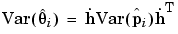
(6-21)

where the dot notation denotes the Jacobian matrix with respect to the response features, 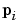. This implies that 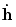is of dimension (pxp). Finally the predicted response values are calculated from

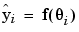
(6-22)

Again, after approximating f by a first order Taylor series and applying the variance operator to the result,

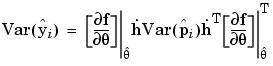
(6-23)

After subsituting Equation 6-19 into Equation 6-23 the desired result is obtained:

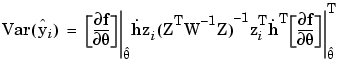
(6-24)

This equation gives the value of Prediction Error Variance.

See also the introduction to Prediction Error Variance for details about PEV for one-stage models.

Two-Stage Models

Global Model Selection