Model Browser User's Guide

Two-Stage Models

To unite the two models, it is first necessary to review the distributional assumptions pertaining to the response feature vector p_i. The variance of p_i (Var(p_i)) is given by

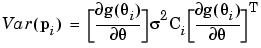
(6-11)

For the sake of simplicity, the notation 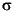²C_i is to denote Var(p_i). Thus, p_ii is distributed as

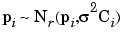
(6-12)

where C_i depends on f_i through the variance of 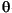_i and also on g_i through the conversion of 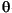_i to the response features p_i. Two standard assumptions are used in determining C_i: the asymptotic approximation for the variance of maximum likelihood estimates and the approximation for the variance of functions of maximum likelihood estimates, which is based on a Taylor series expansion of g_i. In addition, for nonlinear 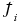or g_i, C_i depends on the unknown 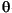_i ; therefore, we will use the estimate 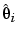in its place. These approximations are likely to be good in the case where 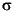² is small or the number of points per sweep (m_i) is large. In either case we assume that these approximations are valid throughout.

We now return to the issue of parameter estimation. Assume that the 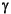_i are independent of the 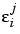. Then, allowing for the additive replication error in response features, the response features are distributed as

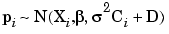
(6-13)

When all the tests are considered simultaneously, equation (6-13) can be written in the compact form

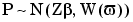
(6-14)

where P is the vector formed by stacking the n vectors p_i on top of each other, Z is the matrix formed by stacking the n X_i matrices, W is the block diagonal weighting matrix with the matrices on the diagonal being 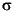²C_i+D , and 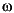is a vector of dispersion parameters. For the multivariate normal distribution (6-14) the negative log likelihood function can be written

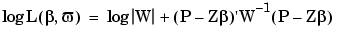
(6-15)

Thus, the maximum likelihood estimates are the vectors 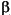_ML and 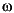_ML that minimize logL(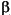,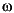).Usually there are many more fit parameters than dispersion parameters; that is, the dimension of 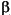is much larger than 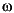. As such, it is advantageous to reduce the number of parameters involved in the minimization of logL(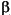,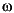). The key is to realize that equation (6-15) is conditionally linear with respect to 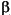. Hence, given estimates of 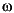, equation (6-15) can be differentiated directly with respect to 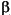and the resulting expression set to zero. This equation can be solved directly for 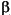as follows:

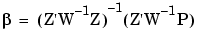
(6-16)

The key point is that now the likelihood depends only upon the dispersion parameter vector 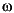, which as already discussed has only modest dimensions. Once the likelihood is minimized to yield 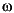_ML , then, since W(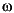_ML) is then known, equation (6-16) can subsequently be used to determine 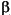_ML.

Global Models

Prediction Error Variance for Two-Stage Models