Model Browser User's Guide    

Global Model Selection

Before undertaking the minimization of Equation 6-15 (see Two-Stage Models) it is first necessary to establish the form of the Xi matrix. This is equivalent to establishing a global expression for each of the response features a priori. Univariate stepwise regression is used to select the form of the global model for each response feature. Minimization of the appropriate PRESS statistic is used as a model building principle, as specified in High-Level Model Building Process Overview. The underlying principle is that having used univariate methods to establish possible models, maximum likelihood methods are subsequently used to estimate their parameters.

Initial Values for Covariances

An initial estimate of the global covariance is obtained using the standard two-stage estimate of Steimer et al. [10],

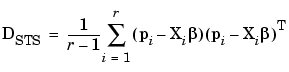
     (6-25)  

where 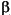are the estimates from all the univariate global models. This estimate is biased.

Quasi-Newton Algorithm

Implicit to the minimization of equation (6-17) is that D is positive definite. It is a simple matter to ensure this by noting that D is positive definite if and only if there is an upper triangular matrix, G, say, such that

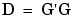
     (6-26)  

This factorization is used in the Quasi-Newton algorithm. Primarily, the advantage of this approach is that the resulting search in G, as opposed to D, is unconstrained.

Expectation Maximization Algorithm

The expectation maximization algorithm is an iterative method that converges toward the maximal solution of the likelihood function. Each iteration has two steps:

  1. Expectation Step -- Produce refined estimates of the response features given the current parameter estimates.
  2. Maximization Step -- Obtain new estimates of the parameters (global model parameters and covariance matrix) for the new response features.

These steps are repeated until the improvement in value of the log likelihood function is less than the tolerance. Details of the algorithm can be found in [3, ch. 5].


  Prediction Error Variance for Two-Stage Models References