Examples of Digital Modulation (Using the Communications Blockset)

Communications Blockset

Examples of Digital Modulation

This section builds a few simple example models to illustrate the modulation methods and how the Communications Blockset allows you to implement them. The examples are:

DQPSK Signal Constellation Points and Transitions

Rectangular QAM Modulation and Scatter Diagram

Phase Tree for Continuous Phase Modulation

Passband Digital Modulation

DQPSK Signal Constellation Points and Transitions

The model below plots the output of the DQPSK Modulator Baseband block. The image shows the possible transitions from each symbol in the DQPSK signal constellation to the next symbol.

To open the completed model, click here in the MATLAB Help browser. To build the model, gather and configure these blocks:

Random Integer Generator, in the Data Sources sublibrary of the Comm Sources library

Set M-ary number to 4.

Set Initial seed to any positive integer scalar, preferably the output of the randseed function.

Set Sample time to .01.

DQPSK Modulator Baseband, in the PM sublibrary of the Digital Baseband sublibrary of Modulation

Complex to Real-Imag, in the Simulink Math Operations library

XY Graph, in the Simulink Sinks library

Use the blocks' default parameters unless otherwise instructed. Connect the blocks as in the figure. Running the model produces the following plot. The plot reflects the transitions among the eight DQPSK constellation points.

This plot illustrates 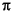/4-DQPSK modulation, because the default Phase offset parameter in the DQPSK Modulator Baseband block is pi/4. To see how the phase offset influences the signal constellation, change the Phase offset parameter in the DQPSK Modulator Baseband block to pi/8 or another value. Run the model again and observe how the plot changes.

Rectangular QAM Modulation and Scatter Diagram

The model below uses the M-QAM Modulator Baseband block to modulate random data. After passing the symbols through a noisy channel, the model produces a scatter diagram of the noisy data. The diagram suggests what the underlying signal constellation looks like and shows that the noise distorts the modulated signal from the constellation.

To open the completed model, click here in the MATLAB Help browser. To build the model, gather and configure these blocks:

Random Integer Generator, in the Data Sources sublibrary of the Comm Sources library

Set M-ary number to 16

Set Initial seed to any positive integer scalar, preferably the output of the randseed function

Set Sample time to .1

Rectangular QAM Modulator Baseband, in the AM sublibrary of the Digital Baseband sublibrary of Modulation

Set Normalization method to Peak Power

AWGN Channel, in the Channels library

Set Es/No to 20

Set Symbol period to .1

Discrete-Time Scatter Plot Scope, in the Comm Sinks library

Select Show Plotting Properties

Set Points displayed to 160

Set New points per display to 80

Select Show Figure Properties

Set Scope position to figposition([2.5 55 35 35]);

Set Figure name to QAM Scatter Plot

Connect the blocks as in the figure. Also, from the model window's Simulation menu, choose Simulation parameters; then, in the Simulation Parameters dialog box, set Stop time to 250. Running the model produces a scatter diagram like the following one. Your plot might look somewhat different, depending on your Initial seed value in the Random Integer Generator block. Because the modulation technique is 16-QAM, the plot shows 16 clusters of points. If there were no noise, the plot would show the 16 exact constellation points instead of clusters around the constellation points.

Phase Tree for Continuous Phase Modulation

This example plots a phase tree associated with a continuous phase modulation scheme. A phase tree is a diagram that superimposes many curves, each of which plots the phase of a modulated signal over time. The distinct curves result from different inputs to the modulator.

This example uses the CPM Modulator Baseband block for its numerical computations. The block is configured so that it uses a raised cosine filter pulse shape. The example also illustrates how you can use Simulink and MATLAB together. The example uses MATLAB commands to run a series of simulations with different input signals, to collect the simulation results, and to plot the full data set.

The first step of this example is to build the model. To open the completed model, click here in the MATLAB Help browser. To build the model, gather and configure these blocks:

DSP Constant, in the DSP Sources library

Set Constant value to s (which will be in the MATLAB workspace)

Set Output to Frame-based

Set Frame period to 1

CPM Modulator Baseband

Set M-ary number to 2.

Set Modulation index to 2/3.

Set Frequency pulse shape to Raised Cosine.

Set Pulse length to 2.

To Workspace, in the Simulink Sinks library

Set Variable name to x.

Set Save format to Array.

Do not run the model, because the variable s is not yet defined in the MATLAB workspace. Instead, save the model to a directory on your MATLAB path, using the filename doc_phasetree.

The second step of this example is to execute these commands in MATLAB.

% Parameters from the CPM Modulator Baseband block
M_ary_number = 2;
modulation_index = 2/3;
pulse_length = 2;
samples_per_symbol = 8;
opts = simset('SrcWorkspace','Current',...
   'DstWorkspace','Current');

L = 5;  % Symbols to display
pmat = [];
for ip_sig = 0:(M_ary_number^L)-1
    s = de2bi(ip_sig,L,M_ary_number,'left-msb');
    % Apply the mapping of the input symbol to the CPM
    % symbol 0 -> -(M-1), 1 -> -(M-2), etc.
    s = 2*s'+1-M_ary_number;
    sim('doc_phasetree', .9, opts); % Run model to generate x.
    pmat(:,ip_sig+1) = unwrap(angle(x(:))); % Next column of pmat
end;
pmat = pmat/(pi*modulation_index);
t = (0:L*samples_per_symbol-1)'/samples_per_symbol;
plot(t,pmat); figure(gcf); % Plot phase tree.

The resulting plot follows. Each curve represents a different instance of simulating the CPM Modulator Baseband block with a distinct (constant) input signal.

Passband Digital Modulation

The example below uses passband phase shift keying modulation and displays the spectrum of the modulated signal. The M-PSK Modulator Passband block's parameters satisfy necessary requirements for passband simulation because

The input signal's sampling rate of 10 is less than the carrier frequency of 100.

The modulated signal's sampling rate of 3000 exceeds the sum of twice the carrier frequency and twice the input sampling rate.

These requirements are mentioned on the reference page for the M-PSK Modulator Passband block.

To open the completed model, click here in the MATLAB Help browser. To build the model, gather and configure these blocks:

Bernoulli Binary Generator, in the Data Sources sublibrary of the Comm Sources library.

Set Probability of a zero to [.5, .5].

Set Initial seed to any row vector containing 2 positive integers, preferably the output of the randseed function.

Set Sample time to .1.

M-PSK Modulator Passband, in the PM sublibrary of the Digital Passband sublibrary of Modulation

Set M-ary number to 4.

Set Input type to Bit.

Set Symbol period to .1.

Set Carrier frequency to 1000.

Set Carrier initial phase to pi/4.

Set Output sample time to 1/3000.

Buffer, in the DSP Blockset Buffers sublibrary of the Signal Management library

Set Output buffer size to 1024.

Magnitude FFT, in the DSP Blockset Power Spectrum Estimation sublibrary of the Estimation library

Check the Inherit FFT length from input dimensions check box.

Mean, in the DSP Blockset Statistics library

Check the Running mean check box.

Set Reset port to None.

Vector Scope, in the DSP Blockset DSP Sinks library

Set Input domain to Frequency.

Check the Axis properties check box.

Set Frequency range to [-Fs/2...Fs/2].

Set Maximum Y-limit to 100.

Connect the blocks as in the preceding figure. Also, from the model window's Simulation menu, choose Simulation parameters; then in the Simulation Parameters dialog box, set Stop time to 10. Running the model produces the following spectral plot.

You might want to vary the modulation technique to see how this plot would change. For example, you can try replacing the M-PSK Modulator Passband block with the M-DPSK Modulator Passband or OQPSK Modulator Passband block.

Upsampled Signals and Rate Changes Selected Bibliography for Digital Modulation