| Aerospace Blockset | |
Convert direction cosine matrix to Euler angles
Library
Description
The Direction Cosine Matrix to Euler Angles block converts a 3-by-3 direction cosine matrix (DCM) into three Euler rotation angles. The DCM matrix performs the coordinate transformation of a vector in inertial axes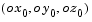 
into a vector in body axes 
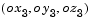. The order of the axis rotations required to bring 
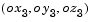into coincidence with 
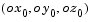is first a rotation about 
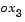through the roll angle 
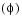to axes 
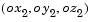. Second a rotation about 
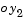through the pitch angle 
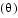to axes 
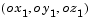, and finally a rotation about 
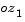through the yaw angle 
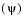to axes 
.
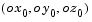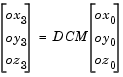
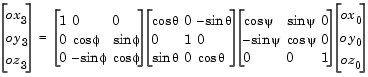
Combining the three axis transformation matrices defines the following DCM.
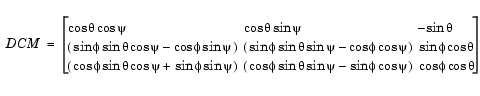
To determine Euler angles from the DCM, the following equations are used:
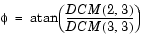
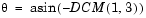
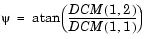
Dialog Box
Inputs and Outputs
The input is a 3-by-3 direction cosine matrix.
The output is a 3-by-1 vector of Euler angles.
Assumptions and Limitations
This implementation generates a pitch angle that lies between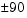 
degrees, and roll and yaw angles that lie between 
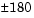degrees.
See Also
Direction Cosine Matrix to Quaternions
Euler Angles to Direction Cosine Matrix
Quaternions to Direction Cosine Matrix
| | Density Conversion | Direction Cosine Matrix to Quaternions | |
