

| Aerospace Blockset |   |
Convert quaternion vector to direction cosine matrix
Library
Description
The Quaternions to Direction Cosine Matrix block transforms the four-element unit quaternion vector (q0,q1,q2,q3) into a 3-by-3 direction cosine matrix (DCM). The outputted DCM performs the coordinate transformation of a vector in inertial axes to a vector in body axes.
Using quaternion algebra, if a point P is subject to the rotation described by a quaternion q, it changes to P' given by the following relationship:
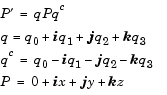
Expanding P' and collecting terms in x, y, and z gives the following for P' in terms of P in the vector quaternion format.
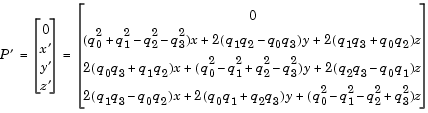
Since individual terms in P' are linear combinations of terms in x, y, and z, a matrix relationship to rotate the vector (x,y,z) to (x',y',z') can be extracted from the preceding. This matrix rotates a vector in inertial axes, and hence is transposed to generate the DCM that performs the coordinate transformation of a vector in inertial axes into body axes.
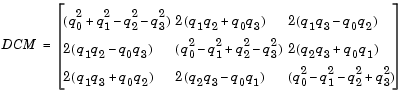
Dialog Box
Inputs and Outputs
The input is a 4-by-1 quaternion vector.
The output is a 3-by-3 direction cosine matrix.
Examples
See aeroblk_six_dof.mdl for an example of the use of the Quaternions to Direction Cosine Matrix block in an implementation of the equations of motion of a rigid body.
See Also
Direction Cosine Matrix to Euler Angles
Direction Cosine Matrix to Quaternions
Euler Angles to Direction Cosine Matrix
 | Pressure Conversion | Quaternions to Euler Angles |  |