| Aerospace Blockset | |
Convert Euler angles to a quaternion vector
Library
Description
The Euler Angles to Quaternions block converts the rotation described by the three Euler angles (roll, pitch, yaw) into the four-element quaternion vector (q0,q1,q2,q3).
A quaternion vector represents a rotation about a unit vector (
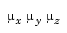) through an angle 
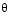. A unit quaternion itself has unit magnitude, and can be written in the following vector format.
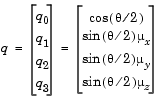
An alternative representation of a quaternion is as a complex number,
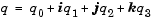
where, for the purposes of multiplication,
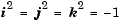
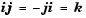
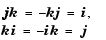
The benefit of representing the quaternion in this way is the ease with which the quaternion product can represent the resulting transformation after two or more rotations. The quaternion to represent the rotation through the three Euler angles is given below.
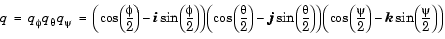
Expanding the preceding representation gives the four quaternion elements following.
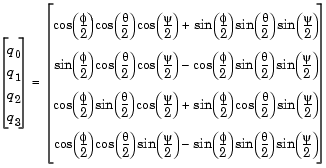
Dialog Box
Inputs and Outputs
The input is a 3-by-1 vector of Euler angles.
The output is a 4-by-1 quaternion vector.
See Also
Direction Cosine Matrix to Euler Angles
Direction Cosine Matrix to Quaternions
Euler Angles to Direction Cosine Matrix
Quaternions to Direction Cosine Matrix
| | Euler Angles to Direction Cosine Matrix | Equations of Motion | |
