

| Aerospace Blockset |   |
Convert direction cosine matrix to quaternion vector
Library
Description
The Direction Cosine Matrix to Quaternions block transforms a 3-by-3 direction cosine matrix (DCM) into a four-element unit quaternion vector (q0,q1,q2,q3). The DCM performs the coordinate transformation of a vector in inertial axes to a vector in body axes.
The DCM is defined as a function of a unit quaternion vector by the following:
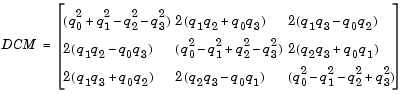
Using this representation of the DCM, there are a number of calculations to arrive at the correct quaternion. The first of these is to calculate the trace of the DCM to determine which set of algorithms are used. If the trace is greater that zero, the quaternion can be automatically calculated. When the trace is less than or equal to zero, the major diagonal element of the DCM with the greatest value must be identified to determine the final algorithm used to calculate the quaternion. Once the major diagonal element is identified, the quaternion is calculated. For a detailed view of these algorithms, look under the mask of the Direction Cosine Matrix to Quaternions block.
Dialog Box
Inputs and Outputs
The input is a 3-by-3 direction cosine matrix.
The output is a 4-by-1 quaternion vector.
See Also
Direction Cosine Matrix to Euler Angles
Euler Angles to Direction Cosine Matrix
Quaternions to Direction Cosine Matrix
 | Direction Cosine Matrix to Euler Angles | Discrete Wind Gust Model |  |