Signal Processing Toolbox

Kaiserウィンドウ

Kaiserウィンドウは、メインロブのエネルギーとサイドロブのエネルギーとの比率が最大となるような扁長回転楕円体ウィンドウに対する近似です。設定した長さのKaiserウィンドウでは、パラメータ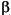がサイドロブの高さを制御します。与えられた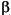に対して、サイドロブの高さは、ウィンドウの長さに関して固定されます。ステートメントkaiser(n,beta)は、パラメータbetaをもつ長さnのKaiserウィンドウを計算します。

長さが50で、betaパラメータにさまざまな値をもつKaiserウィンドウの例は、つぎのようになります。

n = 50;
w1 = kaiser(n,1);
w2 = kaiser(n,4);
w3 = kaiser(n,9);
[W1,f] = freqz(w1/sum(w1),1,512,2);
[W2,f] = freqz(w2/sum(w2),1,512,2);
[W3,f] = freqz(w3/sum(w3),1,512,2);
plot(f,20*log10(abs([W1 W2 W3]))); grid;
legend('beta = 1','beta = 4','beta = 9',3)
title('Three Kaiser ウインドウ Responses')
xlabel('Normalized Frequency (Nyquist = 1)')
ylabel('Normalized Magnitude (dB)')

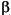が増加するに連れて、サイドロブの高さが減少し、メインロブの幅が増加します。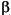パラメータを固定した場合、長さが変化したときに、サイドロブの高さが同じ値に留まるかどうかを確認するには、つぎのようにします。

w1 = kaiser(50,4);
w2 = kaiser(20,4);
w3 = kaiser(101,4);
[W1,f] = freqz(w1/sum(w1),1,512,2);
[W2,f] = freqz(w2/sum(w2),1,512,2);
[W3,f] = freqz(w3/sum(w3),1,512,2);
plot(f,20*log10(abs([W1 W2 W3]))); grid;
legend('length = 50','length = 20','length = 101')
title('Three Kaiser ウインドウ Responses, Beta Fixed')
xlabel('Normalized Frequency (Nyquist = 1)')
ylabel('Normalized Magnitude (dB)')

FIR設計におけるKaiserウィンドウ

Kaiserウィンドウを用いて、フィルタ仕様を満たすFIRフィルタを設計するのに役立つ2つの設計式があります。高さ- dBのサイドロブを達成するには、betaパラメータをつぎのようにします。

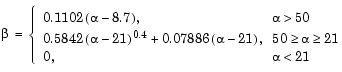
遷移幅が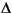ラジアン/秒である場合には、つぎの長さを使用します。

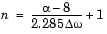
これらの発見的方法を用いて設計されたフィルタは、仕様を、ほぼ満たしますが、これを検証する必要があります。カットオフ周波数0.5ラジアン/秒、および、遷移幅0.2ラジアン/秒をもち、かつ遮断帯域に40 dBの減衰をもつローパスフィルタを設計するには、つぎのようにします。

[n,wn,beta] = kaiserord([0.4 0.6]*pi,[1 0],[0.01 0.01],2*pi);
h = fir1(n,wn,kaiser(n+1,beta),'noscale');

関数kaiserordは、与えられた周波数領域仕様を満たすのに必要なフィルタ次数、カットオフ周波数、およびKaiserウィンドウの beta パラメータを推定します。

通過帯域内のリップルは、遮断帯域内のリップルと、ほぼ同じになります。周波数応答からわかるように、このフィルタは、ほぼ仕様を満たしています。

[H,f] = freqz(h,1,512,2);
plot(f,20*log10(abs(H))), grid

kaiserordの詳細については、第7章のリファレンスを参照してください。

一般化コサインウィンドウ

Chebyshevウィンドウ